1.思维导图

2.数学运算

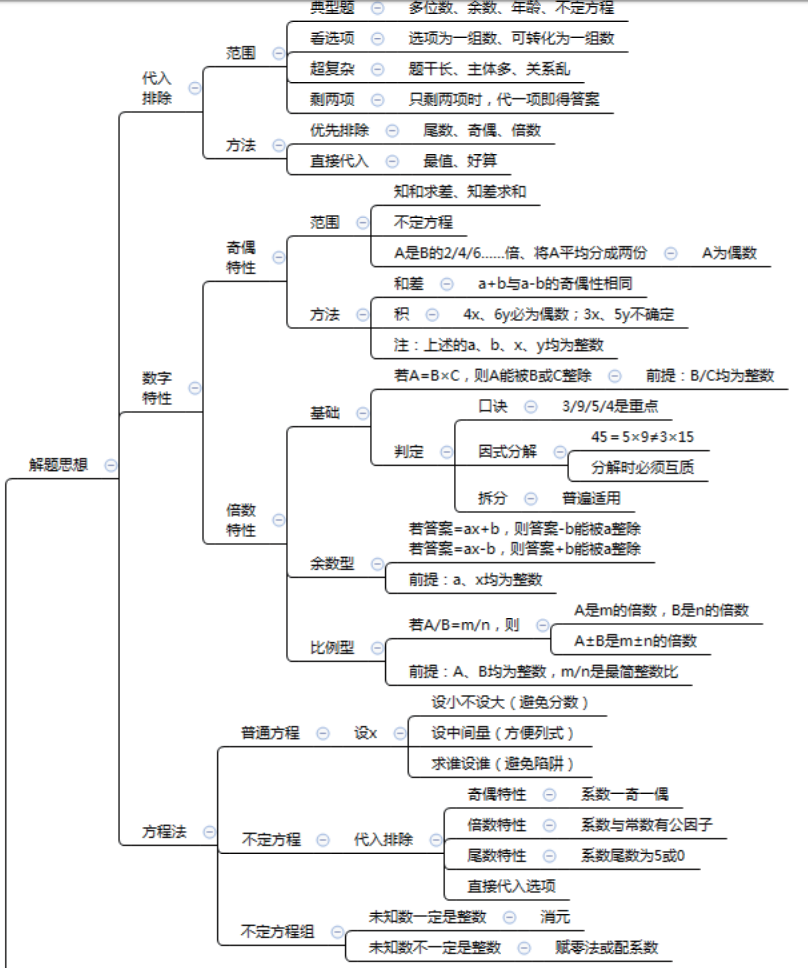
1.代入排除

1.概述

【知识点】代入排除：平时做题都是从题干出发，列式求解，而代入排除 法是将选项代入到题干中，满足则保留，不满足则排除，即从选项切入求解题 目的方法就是代入排除法。一共四个选项，最多代三项即可确定答案，如 A、 B、C 项均错误，则 D 项一定正确。
1.什么时候用？
（1）题型：年龄、余数、不定方程、多位数。
①年龄：涉及到年龄的问题。
②余数:
引例.一个数，除以 7 余 3，除以 8 余 2，除以 9 余 1，问：这个数可能是 几？
A.10 B.11 C.12 D.13
答：将选项代入，A 项：10/7=1„„3，10/8=1„„2，10/9=1„„1，满 足题意，答案选 A 项。
③不定方程：未知数个数多于方程个数。 引例.3x+2y=10，求：x、y 的值。 A.2、2 B.2、3 C.1、4 D.0、4
答：两个未知数一个方程，为不定方程，将选项代入求解，代入 A 项： 32+22=6+4=10，满足题意，答案选 A 项，若 A 项不满足题意，则继续代入， 直到确定答案。
④多位数：如三位数、四位数等位数较多的数或出现位数的变化。 引例.一个三位数，十位和个位对调，比原来大 9，问：这个三位数可能 是几？
A.120 B.121 C.122 D.123 答：从选项切入。A 项：120 的十位数与个位数对调得到 102，比对调前 小，排除；B 项：121 的十位数与个位数对调得到 112，比对调前小，排除；C 项：122 的十位数与个位数对调得到 122，与对调前一样，排除；D 项：123 的 十位数与个位数对调得到 132，132 比 123 大 9，符合题意。
（2）选项：
①选项信息充分：一组数。如一个选项给了两个数，将选项代入即可求解。
②剩二代一。如 A、B、C、D 四个选项，排除 A、B 项后，代入 C 项，满足 题意则选 C 项，不满足则选 D 项，即剩二代一，必得答案。
（3）题干：主体多、条件复杂，尝试代入。要么跑，要么代入排除求解。
2.怎么用？
（1）先排除（如有四个选项，代入三项比较慢，但若先排除两个选项后， 只需要代入一项即可确定答案）：奇偶、倍数、尾数。
（2）再代入：
①最值原则。一个数是 15 的倍数，选项为：A.15，B.30，C.31，D.45， 问这个数最大是多少？即使 A、B、C、D 项均符合条件，也需要选最大的，因 此问最大，从最大的开始代，既快又不容易出错。
②从简原则。A.99，B.100，C.101，D.102，优先代入好算的 100

2.举例

例 2（2017 江西）3 年前张三的年龄是他女儿的 17 倍，3 年后张三的年龄是 他女儿的 5 倍，那么张三的女儿现在（ ）。
A.2 岁 B.3 岁 C.4 岁 D.5 岁
本题为年龄问题，考虑代入排除法。
例 4（2017 广州）几个朋友相约游泳，男士统一戴白色泳帽，女士统一戴红 色泳帽。每位男士看到的白色泳帽数量与红色泳帽数量一样多，每位女士看到的 白色泳帽数量都是红色泳帽数量的倍数。女士最少有（ ）人。
A.1 B.2 C.3 D.4
【解析】白色-1=红色，白色=（红色-1）*n。观察发现算式不好求解，且不会解，考虑代入排 除法。题干问“最少”，从最少的选项开始代，代入 A 项验证：红色=1，白色=2， 1-1=0，2 不是 0 的倍数，不满足题意，排除；代入 B 项验证：红色=2，白色=3， 2-1=1，3 是 1 的倍数，满足题意，当选。【选 B】

1. 数字特性法

1.奇偶特性-概述

①在加减法中，同奇同偶则为偶，一奇一偶则为奇。如 5+3=8，5-3=2；5 -4=1，5+4=9
②a+b 与 a-b 的奇偶性相同（和差同性）。如 5+3 为偶数， 5-3 一定为偶数； 如 3+2 为奇数，3-2 一定为奇数；4+2=6 为偶数，4-2=2 为偶数。
（3）引例.共 50 题，答对得 3 分，答错倒扣 1 分，共得 82 分，问答对的 题和答错的题相差多少道？
A.16 B.17 C.31 D.33
在乘法中，一偶则偶，全奇为奇。
3.什么时候用？
（1）不定方程，首先考虑奇偶特性。
（2）知和求差、知差求和。
（3）平分成 2 份（奇数+奇数=偶数，偶数+偶数=偶数）、偶数倍（如 4x、 6y）。
4.怎么用？
（1）加减：和差同性——a+b 与 a-b 奇偶性相同。
（2）乘：4x、6y 必为偶数；3x、5y 奇偶性不确定。

2.奇偶特性-举例

例 1（2017 辽宁）母亲现在的年龄个位数跟十位数对调再减 10 岁就是儿子 的年龄，再过 3 年母亲的年龄就是儿子年龄的 2 倍，则母亲现在的年龄是（ ）。
A.53 B.52 C.43 D.42 【解析】例 1.判定题型，年龄问题，考虑代入排除法，要想快，先排再代。 题中出现“2 倍”，即母亲+3=（儿子+3）2，年龄一定是整数，则（儿子+3）2 是偶数，（母亲+3）是偶数，3 为奇数，则母亲的年龄为奇数（同奇同偶才为偶）
例 2（2015 联考）每年三月某单位都要组织员工去 A、 B 两地参加植树活动， 已知去 A 地每人往返车费 20 元，人均植树 5 棵，去 B 地每人往返车费 30 元，人 均植树 3 棵，设到 A 地有员工 x 人，A、B 两地共植树 y 棵，y 与 x 之间满足 y=8 x–15，若往返车费总和不超过 3000 元时，那么，最多可植树多少棵？（ ）
A.498 B.400 C.489 D.500
【解析】例 2.本题看起来比较复杂，但题中已知 y=8x-15，分析不定方程， 考虑奇偶特性，15 是奇数，8x 是偶数，偶数-奇数=奇数，则 y 为奇数，排除 A、 B、D 项，答案选 C 项。【选 C】 【注意】若选项中有两个奇数时，则代入验证。

3.倍数特性-概述

1.整除基础知识：若 A=BC（B、C 均为整数），则：
（1）A 能被 B 或 C 整除。
（2）B 和 C 均是 A 的约数。
（3）3 的倍数：各位数字相加能被 3 整除，则这个数能被 3 整除。如 12， 各位数字之和为 3如 36，各位数字之和为 9；如 123456，各位数字之和=1+2+3+4+5+6=21
（4）9 的倍数：各位数字相加能被 9 整除，则这个数能被 9 整除。如 18、27、45，各位数字之和均为 9， 如 99963，各位数字之和是 9 的倍数，则 99963 能被 9 整除.
（5）5 的倍数：只看末一位，末一位是 0 或 5 的倍数则能被 5 整数。5 奇数尾数为 5，5偶数尾数为 0。如 53=15，54=20
（6）4 的倍数：看末两位能否被 4 整除（整百的数一定是 4 的倍数）。如 124，末两位为 24，24 能被 4 整除，则 124 能被 4 整除;
（7）不好用口诀的数，考虑因式分解。如 6=23，一个数既是 2 的倍数 又是 3 的倍数，一定能被 6 整除，如 132 既是 2 的倍数又是 3 的倍数，则 132 一定能被 6 整除；注意：拆分出的两个数一定要互质（没有除了 1 以外的公约数）
（8）拆分法：如 602，623，628，631，判定以上数字能否被 7 整除，考 虑拆分：602=630-28，623=630-7，628=630-2，631=630+1。630 一定是 7 的 倍数，28 是 7 的倍数，则 602 是 7 的倍数；7 是 7 的倍数，则 623 是 7 的倍数；

2.倍数特性-举例

例 1（2017 福建）如下图，一个正方体的表面上分别写着连续的 6 个整数， 且每两个相对面上的两个数的和都相等，则这 6 个整数的和为（ ）。
A.53 B.52 C.51 D.50
【解析】例 1.90%的同学做题时的第一反应是找数，但这样做就进入误区了， 从问题入手，问的是“和”，则只看和，已知“每两个相对面上的两个数的和都 相等”，设相对面数字之和为 X，则上+下=左+右=前+后=X，因此总和=3X，可知 总数是 3 的倍数，只有C符合。

【知识点】比例型：如班上男生：女生=3：5，则男生有 3n 人，女生有 5n
人，即男生是 3 的倍数，女生是 5 的倍数；或男生有 3 份的人，女生有 5 份的人。
男生+女生是 3+5=8 份，即总人数是 8 的倍数，女生-男生=5-3=2 份，即男、女
生人数之差为 2 的倍数

例 3（2017 新疆）甲、乙两个班各有 30 多名学生，甲班男女生比为 5：6， 乙班男女生比为 5：4，则甲、乙两班男生总数比女生总数（ ）。
A.多 1 人 B.少 1 人 C.多 2 人 D.少 2 人
【解析】例 3.读完题干，出现分数的比例关系，想到倍数特性。已知甲、 乙两个班各有 30 多名学生，30 多指的是 31～39 人。根据比例关系，甲班：男/ 女=5 份/6 份，总人数是 30 多人，总人数=男生+女生=11 份，总人数是 30 多又 是 11 的倍数，所以甲班是 33 人。甲班：男生=335/11=15 人，女生=336/11=18 人。乙班：男生/女生=5 份/4 份，总人数是 30 多人，总人数=男生+女生=9 份， 总人数是 30 多又是 9 的倍数，只能乙班是 36 人。乙班：男生=365/9=20 人， 女生=364/9=16 人。两班男生的和-两班女生的和=（15+20）-（18+16）=35-34=1 人，多 1 人，对应 A 项。【选 A】

【注意】1.看见分数、百分数比例关系，想到倍数特殊。 
2.给出总人数范围，比如 a/b，先通过比例算出总人数，再求具体值

例 4（2016 北京）某单位原拥有中级及以上职称的职工占职工总数的 62.5%。 现又有 2 名职工评上中级职称，之后该单位拥有中级及以上职称的人数占总人数 的 7/11。问该单位原来有多少名职称在中级以下的职工？（ ）
A.68 B.66 C.64 D.60
【解析】例 4.出现分数的比例关系，考虑用倍数特性做题。依题意得，中级 以上/总人数=62.5%，62.5%=50%+12.5%=1/2+1/8=5/8，即中级以上/总人数=5 份 /8 份；总人数不变，问的是中级以下的职工，则中级以下/总人数=3 份/8 份， 中级以下是 3 的倍数，排除 A、C 项。剩下 B、D 项，代入其中一项进行排除，就 简原则，代入 D 项：3 份对应中级以下是 60 人，8 份对应的总人数是 160 人，中 级以上是 100 人。后面中级以上多 2 人，中级以上/总人数=7/11，102/106≠7/ 11，排除 D 项，对应 B 项。

【知识点】余数型：之前考查了 y=3x，A/B=m/n 的形式。出题人不可能照搬
原题，会变形。 
1.若答案=ax±b，则答案∓b 能被 a 整除。（a、x 均为整数）。 
（1）例：苹果每人分 10 个，还剩 3 个，则苹果个数？ 
答：设人数为 x，总人数=10x+3，总数-3=10x，此时苹果个数（总数-3）为
10 的倍数。 
（2）例：苹果每人分 10 个，还缺 3 个，则苹果个数？ 
答：设人数为 x，总数=10x-3，可以将原式化为总数+3=10x。 
2.出现平均分组有余数的时候，考查余数型

例 5（2016 深圳）两箱同样多的蛋黄派分别分发给两队志愿者做早餐，分给 甲队每人 6 块缺 8 块，分给乙队每人 7 块剩 6 块，已知甲队比乙队多 6 人，则一 箱蛋黄派有（ ）块。
A.120 B.160 C.180 D.240 【解析】例 5.本题是均分组有余数，为余数型问题。设有 x 块蛋黄派，总 人数=6x-8，总人数+8=6x。利用倍数特性，说明总人数+8 是 6 的倍数。 6 的倍数， 因式分解， 6=23，说明答案+8 既是偶数又是 3 的倍数，四个选项+8 后都是偶数， 只有 B 项+8 是 3 的倍数，对应 B 项。【选 B】
例 6（2014 广东）在某公司年终晚会上，所有员工分组表演节目。如果按 7 男 5 女搭配分组，则只剩下 8 名男员工；如果按 9 男 5 女搭配分组，只剩下 40 名女员工。该公司员工总数为（ ）。
A.446 B.488 C.508 D.576
【解析】例 6.问公司员工的总数，依题意得，设有 x 组，（7 男+5 女）x+8 男=总人数，可以只看人数不看性别，总人数=12x+8，总人数-8=12x。利用倍数 特性，说明选项-8 是 12 的倍数，因式分解 12=34，说明选项-8 应该是 3 和 4 的公倍数。代入排除，选项-8 后是 3 的倍数，只有 A、B 项满足，排除 C、D 项； 剩下两项，代入 A 项：446-8=438，不是 4 的倍数，排除 A 项，只有 B 项符合。 【选 B】

4.方程法-概述

1.普通方程：设 x。
（1）设小不设大（避免分数）。
（2）设中间量（方便列式）。
（3）求谁设谁（避免陷阱）。
2.不定方程：代入排除。
（1）奇偶特性：系数一奇一偶。
（2）倍数特性：系数与常数有公因子。
（3）尾数特性：系数尾数为 5 或者 0。
（4）直接代入选项。
3.不定方程组：
（1）未知数一定是整数，消元。例如人数，书本数。
（2）未知数不一定是整数，赋零法或配系数（先用赋零，不理解这种方法 的多多练习一下）

5.方程法-举例

例 2（2017 江西）某人雇佣了甲、乙、丙三名工人加工一批零件，其中有 8 7 个零件不是甲加工的，有 86 个零件不是乙加工的，有 85 个零件不是丙加工的， 那么甲加工的零件数是（ ）。
A.42 个 B.43 个 C.44 个 D.45 个
【解析】例 2.根据题意，整理得：乙+丙=87①，甲+丙=86②，甲+乙=85③， 三个方程，三个未知数。把三个方程相加，2（甲+乙+丙）=863，化简得：甲+ 乙+丙=43*3=129④。由④-①得，解得甲=42。【选 A】

【知识点】不定方程组： 
1.第一类：未知数一定是整数的不定方程组。例如人数，书本数。 
2.方法：先消元转化为不定方程。例：a1X+b1Y+c1Z=M①，a2X+b2Y+c2Z=N②，
先消元，转化成 ax+by=z 的形式。再按不定方程求解。

例 4（2017 江苏）某地遭受重大自然灾害后，A 公司立即组织捐款救灾。已 知该公司有 100 名员工捐款，捐款额有 300 元、500 元和 2000 元三种，捐款总 额为 36000 元，则捐款 500 元的员工数是（ ）。
A.11 人 B.12 人 C.13 人 D.14 人 【解析】例 4.总共有三类员工，分别设捐款 300 的人数为 a 人，捐款 500 的人数为 b 人，捐款 2000 的人数为 c 人，列式为：a+b+c=100①，300a+500b+2 000c=36000②，两个方程三个未知数，是不定方程组，用消元法进行求解。求谁 保留谁，问题求 b 要保留 b。化简②式得：3a+5b+20c=360③；由①*3 得：3a+3 b+3c=300④。由③-④得：2b+17c=60，60 和 2b 都是偶数，说明 17c 一定是偶数。 17 是奇数，则 c 是偶数，解得 c=2，则 2b=26，b=13。【选 C】

【知识点】不定方程组： 
1.第二类：未知数不一定是整数的不定方程（组），求的是时间、金钱，未
知数不是整数，解太多。 
2.方法： 
（1）赋零法：对于未知数不一定是整数的不定方程组，可以赋其中 1 个未
知数为 0，进而快速计算出其他未知数。例如 a+3b+2c=0，2a+8b+12c=0，可以赋
值任意一个数为 0。 
（2）配系数。

例 5（2016 联考）木匠加工 2 张桌子和 4 张凳子共需要 10 个小时，加工 4 张桌子和 8 张椅子需要 22 个小时。问如果他加工桌子、凳子和椅子各 10 张，共 需要多少小时？（ ） A.47.5 B.50 C.52.5 D.5 【解析】例 5.设加工 1 张桌子为 a 小时，加工 1 张凳子为 b 小时。，加工 1 张椅子 c 小时，整理等量关系得：2a+4b=10①，4a+8c=22②。两个方程三个未知 数。
方法一：配系数。①2 得：4a+8b=20③，②+③得：8a+8b+8c=42，整理得 8 （a+b+c）=42，求的时间是 10 的倍数，则 4210/8=52.5 小时。 方法二：赋零法。2a+4b=10①，4a+8c=22②。设时间不一定是整数，赋值 a=0， 解得 b=2.5， c=2.75。a+b+c=0+2.5+2.75=5.25，时间=5.2510=52.5。【选 C】 【注意】未知数不是整数的情况，有无数组的解，问题问的是时间，答案是 固定的，只需要找最简单的解，赋值为 0 是最简单的。
例 6（2018 上海）现有甲、乙、丙三种货物，若购买甲 1 件、乙 3 件、丙 7 件共需 200 元；若购买甲 2 件、乙 5 件、丙 11 件共需 350 元，则购买甲、乙、 丙各 1 件共需（ ）元。
A.50 B.100 C.150 D.200
【解析】例 6.问购买甲、乙、丙各 1 件共需的钱数，分别设甲、乙、丙各 1 件的钱数为 a、b、c，根据题意，a+3b+7c=200①，2a+5b+11c=350②。因为钱数 不一定是整数，用赋零法，c 最麻烦，赋 c=0，则 a+3b=200③，2a+5b=350④， ③2 得：2a+6b=400⑤，由⑤-④，解得 b=50，a=50。求出总的价钱=a+b+c=50+ 50+0=100。【选 B】

3.工程问题+行程问题+溶液问题

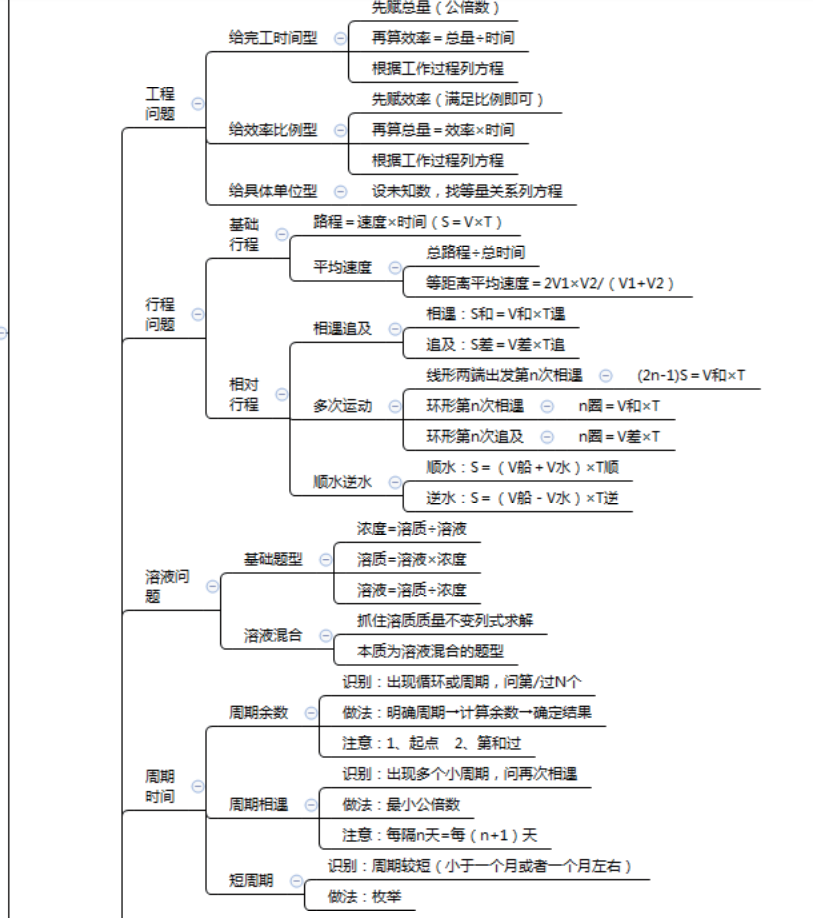
1.工程问题

1.概述

1.三量关系：总量=效率*时间。
例：老师每小时搬砖 10 块，则 5 小时搬砖 50 块；或老师搬砖 50 块，耗时 5 小时，则老师每小时搬砖 10 块。
2.切入点：
（1）给定完工时间型。
（2）给定效率比例型。
（3）给定具体单位型。

1.给定完工时间型：

1.方法：
（1）先赋总量（时间的公倍数）。
（2）再算效率=总量/时间。
（3）根据题意完成工作。
2.例：搬完一车砖，小成需要 2 小时，小刘需要 3 小时，现俩人合作，需要 多久？
答：小学、初中学习时会把总量设为 1，则小成效率 1/2，小刘效率 1/3， 此时出现分数，计算较复杂；为方便计算，往往赋值总量为完工时间的公倍数。 赋总量为 2 和 3 的公倍数 6，则小成效率=总量/小成完工时间=6/2=3，小刘效率 =总量/小刘完工时间=6/3=2，所以合作需要的时间=总量/（小成效率+小刘效率） =6/（3+2）=6/5=1.2 小时

2.举例

例 1（2014 江苏）有一项工程，甲、乙、丙分别用 10 天、15 天、12 天可独 自完成。现三人合作，在工作过程中，乙休息了 5 天，丙休息了 2 天，甲一直坚 持到工程结束，则最后完成的天数是（ ）。
A.6 B.9 C.7 D.8
【解析】例 1.根据“甲、乙、丙分别用 10 天、15 天、12 天可独自完成”， 确定题目属于给定完工时间型工程问题。三步走：（1）赋总量：赋总量为 10、 15、12 的公倍数60。（ 2）求效率：甲效率=60/10=6，乙效率=60/15=4，丙效率=60/12=5。 （ 3）再做题：设甲工作了 t 天，根据“在工作过程中，乙休息了 5 天，丙休息了 2 天，甲一直坚持到工程结束”列方程：6t+4* （t-5）+5*（t-2）=60，整理得：15t=90，解得 t=6，对应 A 项。【选 A】
例 2（2017 国考）工厂有 5 条效率不同的生产线。某个生产项目如果任选 3 条生产线一起加工，最快需要 6 天整，最慢需要 12 天整；5 条生产线一起加工， 则需要 5 天整。问如果所有生产线的产能都扩大一倍，任选 2 条生产线一起加工 最多需要多少天完成？（ ）
A.11 B.13 C.15 D.30
】切入点：给定完工时间型。 1.赋总量：6、12、5 的公倍数：60。 2.求效率：假设 5 条生产线从快到慢：a＞b＞c＞d＞e。 （1）最快 6 天（3 条最快）：a+b+c=60/6=10。 （2）最慢 12 天（3 条最慢）：c+d+e=60/12=5。 （3）五条一起：a+b+c+d+e=60/5=12。 3.再做题：任选 2 条，加工时间最长即效率最低（选最慢的两条 d+e）。

1.给定效率比例型

1.方法：
（1）赋效率（满足比例即可）。
（2）算总量：效率时间=总量。
（3）根据题意完成工作。
2.例：搬一堆砖，小成和小刘的效率比为 2：1，合作 3 小时完成，若交给 小成单独做，问小成需要做多少小时？
答：三步走：（1）赋效率：根据已知效率比，赋小成、小刘的效率分别为 2、 1，也可以赋其他值，但一般是几就赋几最简便。（2）算总量：总量=（2+1）3=9。 （3）根据题意完成工作：总量/效率=时间，则小成单独做需要 9/2=4.5 小时

2.举例

例 3（2016 深圳）甲、乙二人同时上山砍柴，甲花 6 小时砍了一担柴，乙砍 了一段时间后觉得刀比较钝，于是下山磨了一次刀，磨刀加上山下山共花了一个 小时，磨完后效率提升 50%，总共也花费了 6 个小时砍了同样一担柴，如果甲、 乙二人磨刀之前的效率是相同的，则乙磨刀之前已经砍了（ ）个小时柴。
A.1 B.2 C.3 D.4
【解析】例 3.根据“磨完后效率提升 50%”“ 甲、乙二人磨刀之前的效率是 相同的”，确定题目为给定效率比例型工程问题。三步走：（1）赋效率：根据“甲、 乙二人磨刀之前的效率是相同的”“ 磨完后效率提升 50%”，赋甲效率为 1，乙磨 刀前效率为 1、乙磨刀后的效率为 1.5。（2）求总量：根据“甲花 6 小时砍了一 担柴”，则总量=61=6。（ 3）再做题：设乙磨刀前砍柴 t 小时，注意“磨刀加上 山下山共花了一个小时”，根据题意列方程：1t+1.5（6-1-t）=6，整理得： 0.5t=1.5，解得 t=3，对应 C 项。【选 C】
例 4（2017 北京）某检修工作由李和王二人负责，两人如一同工作 4 天，剩 下工作量李需要 6 天，或王需要 3 天完成。现李和王共同工作了 5 天，则剩下的 工作李单独检修还需几天完成？（ ）
A.2 B.3 C.4 D.5
【解析】例 4.已知条件虽然出现了时间，但并不是完成工作总量所需的时 间，所以题目不是给定完工时间型工程问题；根据“剩下工作量李需要 6 天，或 王需要 3 天完成”，即 6李效率=3王效率，说明李效率：王效率=1：2，确定题 目应为给定效率比例型工程问题。三步走： （1）赋效率：赋李效率为 1，王效率 为 2。（ 2）求总量：根据“两人如一同工作 4 天，剩下工作量李需要 6 天，或王 需要 3 天完成”，则总量=（1+2）4+61=18。（ 3）再做题：根据“现李和王共同 工作了 5 天”， 设剩下的工作李单独检修还需 t 天，列方程：（1+2）5+t1=18， 整理得：15+t=18，解得 t=3，对应 B 项。【选 B】
例 5（2018 国考）工程队接到一项工程，投入 80 台挖掘机。如连续施工 30 天，每天工作 10 小时，正好按期完成。但施工过程中遭遇大暴雨，有 10 天时间 无法施工。工期还剩 8 天时，工程队增派 70 台挖掘机并加班施工。问工程队若 想按期完成，平均每天需多工作多少个小时？（ ）
A.1.5 B.2 C.2.5 D.3
【解析】例 5.出现机器，默认每台机器效率相同，确定题目为给定效率比 例型工程问题。三步走： （1）赋效率：每台挖掘机效率为 1。（ 2）求总量：总量 =8030101。（3）再做题：根据“有 10 天时间无法施工”“ 工期还剩 8 天时”， 说明还剩下 18 天的工作量，即还剩下的工作量=8018101；根据“工程队增派 70 台挖掘机并加班施工”，此时效率=80+70=150；设增派挖掘机后每天工作 t 小 时，根据“按期完成”列方程：8018101=1508t1，整理得：180=15t，解 得 t=12，所以每天多干 12-10=2 小时，对应 B 项。【选 B】
例 6（2018 浙江）某蛋糕店接到 300 个蛋糕的订单。已知老板一天能做 30 个蛋糕，店员小红一天只能做 10 个。蛋糕制作过程中，老板有一个周末外出， 小红请了 8 天假，两人在外时间不重叠。问制作这批蛋糕一共花了多少天？（ ）
A.11 B.12 C.13 D.14
【解析】例 6.出现具体单位，确定题目为给定具体单位型工程问题。根据 “蛋糕制作过程中，老板有一个周末外出，小红请了 8 天假，两人在外时间不重 叠”，说明老板 2 天没工作、小红 8 天没工作，且每天都有人工作，设制作这批 蛋糕一共花了 t 天，则老板工作了（t-2）天，小红工作了（t-8）天，列方程： 300=30（t-2）+10*（t-8）， 整理得：40t=440，解得 t=11，对应 A 项。【选 A】

2.行程问题

1.基础行程

1.概述

1.普通行程：
（1）路程=速度时间（S=VT）。 火车过桥问题：路程=桥长+车长。
（2）平均速度：
①总路程/总时间；
②等距离平均速度=2V1V2/（V1+V2）。

2.举例

例 1（2015 江苏）一列火车途经两个隧道和一座桥梁，第一个隧道长 600 米，火车通过用时 18 秒；第二个隧道长 480 米，火车通过用时 15 秒；桥梁长 800 米，火车通过时速度为原来的一半，则火车通过桥梁所需的时间为（ ）。
A.20 秒 B.25 秒 C.40 秒 D.46 秒 【解析】例 1.火车过桥问题，路程=桥长+车长=速度（v）时间（t）。根据 “第一个隧道长 600 米，火车通过用时 18 秒”， 则 600+车长=18V①；根据“第 二个隧道长 480 米，火车通过用时 15 秒”，则 480+车长=15V②，① -②得，120=3V， 解得 V=40 米/秒③，③代入②得，车长=120 米。设所求过桥时间为 t，根据“桥 梁长 800 米，火车通过时速度为原来的一半”，则 800+120=40/2t，整理得： 920=20t，解得 t=46，对应 D 项。【选 D】
例 2（2018 国考）一辆汽车第一天行驶了 5 个小时，第二天行驶了 600 公里， 第三天比第一天少行驶 200 公里，三天共行驶了 18 个小时。已知第一天的平均 速度与三天全程的平均速度相同，问三天共行驶了多少公里？（ ）
A.800 B.900 C.1000 D.1100
【解析】例 2.出现“已知第一天的平均速度与三天全程的平均速度相同”， 考虑公式：V=S/t。根据“第一天的平均速度与三天全程的平均速 度相同”列方程：（x+200）/5=（x+200+600+x）/18，解得 x=50。所求三天总路程=x+200+600+x=50+200+600+50=900 公里，对应 B 项。【选 B】
例 3（2015 政法干警联考）甲去北京出差，去时坐飞机，返回时坐高铁。若 飞机的速度比高铁快 3 倍，且往返平均速度为 480 千米/小时，问甲乘坐的飞机 速度为多少千米/小时？（ ）
A.720 千米/小时 B.768 千米/小时 C.960 千米/小时 D.1200 千米/小时
【解析】往返距离相等，所以考虑等距离平均速度公式：V=2V1V2/（V1+V2）。 根据 “飞机的速度比高铁快 3 倍”， 则飞机的速度是高铁的 4 倍；设高铁速度为 x， 飞机速度为 4x,代入等距离平均速度 公式：2V1V2/（V1+V2）=24xx/（4x+x）=480，整理得 8x/5=480，解得 x=300 千米/小时，则飞机速度=4x=4*300=1200 千米/小时，对应 D 项。【选 D】 【注意】“快 3 倍”应为“是 4 倍”，避免陷阱。

3.相对行程

【知识点】直线相遇：
1.环境：两人同时同向而行（一人在左，一人在右，然后在中间某位置相遇）。
2.公式：S 和=（V1+V2）t。S 和：两人一起跑的距离。
3.（1）例：小黑和小白两人，一人速度为 V1，另一人速度为 V2，最终在中 点相遇，求总路程？
答：则小黑走的路程为 V1t，小白走的路程为 V2t，则路程和S=V1t+V2t=（V1+V2） *t。
【知识点】环形相遇（同点出发）：
1.例：老师和你两个人，老师往左走，你往右走，最后在图中所示位置相遇， 假设老师速度为 V1，你的速度为 V2，我走的路程是 V1t，你走的路程是 V2t，则合 走的路程 S 和=（V1+V2）t。合走的距离为 1 圈，一圈的长度=（V1+V2）t，相当 于相遇 1 次走了 1 圈。
【知识点】直线追及（两人，一人在前，一人在后，后面的人跑得快，追上 了前面的人） ：
1.例：小白和小黑跑步，小白在前，小黑在后，小黑速度是 V1，小白速度是 V2，小黑跑了 V1t，小白跑了 V2t，最终两人相遇了，之前两人有路程差（假如两 人相距 10 米，最后把 10 找回来，才能追上），后面追上了，路程差 S 差=V1t-V2t= （V1-V2）t。
【知识点】环形追及（同点出发）：
1.例子：假设老师和你在操场跑步，老师跑的较快，你跑的较慢，老师在环 形上追到了你，则老师比你多跑一圈，S 差=（V1-V2）t。
2.公式：S 差=（V1-V2）t。
3.追上一次，S 差=1 圈；追上 N 次，S 差=N 圈。
【知识点】多次相遇（直线上，一个左端，一个右端，两端出发）：
1.例子：牛郎和织女都从家里出发，两人相遇走了 1 个全程，两人见面，话 不投机，吵了一架，分别继续往前走，走到了对方的家，又回去找对方，返回来 再见面，此时会出现第二次相遇，两人共走了 3 个全程。再返回，两人共走 5 个全程。结论：第 n 次相遇走（2n-1）个全程。
【知识点】流水行船：V 顺、V 逆、V 船、V 水。
1.船顺流而下会比平时快，V 顺=V 船+V 水。
2.船逆流而上，V 逆=V 船-V 水。
3.注意：静水速度（水没有速度，V 水=0，只有船速）=船速，漂流速度（顺 着水漂，V 船=0，只有水速）=水速

3.溶液问题

1.概述

【知识点】溶液问题：
1.假如有 10g 盐融到 90g 水中，变成 100g 盐水，盐为溶质，水为溶剂，盐 水为溶液。
2.公式：
（1）溶液=溶质+溶剂，10g+90g=100g。
（2）浓度=溶质/溶液，10g/100g=10%。
（3）溶质=溶液浓度，100g10%=10g。
（4）溶液=溶质/浓度，10g/10%=100g。

2.举例

例 1（2017 上海）实验室使用浓度为 2%的盐水和蒸馏水，配制浓度为 1%的 淡盐水。现有 1000 克蒸馏水和 500 克浓度为 2%的盐水，则最多可配制（ ）克 浓度为 1%的淡盐水。
A.500 B.1000 C.1500 D.2000 【解析】例 1.方法一：蒸馏水为纯水，即 0%浓度的水。求最多可配制多少 浓度为 1%的淡盐水，盐水为溶液，要求溶液，由公式：溶液=溶质/浓度，溶质 未知，由公式溶质=溶液浓度，浓度为 2%的盐水 500g，则溶质=500g2%=10g， 溶液=溶质/浓度=10g/1%=1000g。不着急选答案，先检验：1000g 包括 500g 浓度 为 2%的盐水加上 500g 浓度为 0%的纯净水，混合后浓度为 1%，对应 B 项
【知识点】等溶液混合：
1.例子：假如 500g 浓度为 100%的溶液和 500g 浓度为 0%的溶液混合，混合 后会变成 50%；500g 浓度为 40%的盐水和 500g 浓度为 60%的盐水混合，混合后浓 度会变成（40%+60%）/2=50%；500g 浓度为 50%的盐水和 500g 浓度为 30%的盐水 混合，混合后浓度会变成（50%+30%）/2=40%。
2.推导：假如 500g 浓度为 a%的溶液和 500g 浓度为 b%的溶液，浓度=溶质/ 浓度=（500a%+500b%）/1000=（a%+b%）/2。溶质=溶液*浓度。
3.公式：等量溶液混合最终浓度=（a%+b%）/2。

4.周期问题

1.概述

1.周期余数：
（1）识别：出现循环或周期，问第/过 N 个。
（2）方法：明确周期——计算余数——确定结果。
（3）做法：
①明确周期：定起点和周期数。 ②计算余数：总数/周期数。 ③利用余数确定结果：第 N 个——余几数几；过 N 个——余几加几。 （4）第/过的区别：
①例：周一、二、三、四、五，从周一开始，第 1 天是周一，过 1 天是周 二；从周一开始，第 3 天是周三，过 3 天是周四。过 n 天=第 n 天+1。 ②注意：问“第”时，余几数几；问“过”时，余几加几。
（4）例 1：一排气球按照红白蓝的顺序循环排列，第 29 个什么颜色？ 答：明确周期：按照红白蓝的顺序循环排列，周期是 3；计算余数：总数 /周期数=29/3=9……2；按红、白、蓝的顺序循环了 9 组，最后余 2 个（红白）， 余 2 数 2，则第 29 个是白色。
例 2：今天是礼拜四，再过 29 天是礼拜几？
答：每周都是 7 天，是一个循环，问过 29 天是礼拜几，为周期余数问题。 明确周期：星期的周期是 7；计算余数：29/7=4……1；问“过”，余几加几， 周四+1=周五。
2.周期相遇。
3.短周期。

2.举例

例 1（2016 上海）文化广场上从左到右一共有 5 面旗子，分别代表中国、德 国、美国、英国和韩国。如果将 5 面旗子从左到右分别记作 A、B、C、D、E，那 么从中国的旗子开始，按照 ABCDEDCBABCDEDCBA……的顺序数，数到第 313 个字 母时，是代表（ ）的旗子。
A.英国 B.德国 C.中国 D.韩国 【解析】例 1.题干给出一个循环，问第几个，判定题型为周期余数问题。
（1）明确周期：定起点——A，周期数——8。
（2）计算余数：总数/周期数 313/8=39……1。
（3）确定结果：第 313 个从 A 开始数 1 个，故第 313 个字母是 A 对应中国。【选 C】
例 2（2014 山西、四川）五名工人按甲—乙—丙—丁—戊的顺序轮流值夜班， 每人值班 1 天休息 4 天。某日乙值夜班，问再过 789 天该谁值班？（ ）
A.甲 B.乙 C.丙 D.戊
【解析】例 2.“每人值班 1 天休息 4 天”为一个循环，问再过 789 天该谁 值班，周期余数问题。（1）明确周期，5 个人一人一天，周期为 5。（ 2）计算余 数，789/5=（785+4）/5，785/5 余 0，4/5 余 4，余数是 4。注意乙是起点，从乙开始数过 4 天为甲。【选 A】

【知识点】周期相遇（套路题）： 
1.识别：出现多个小周期，问再次相遇。 
2.做法：最小公倍数，再按周期余数计算。 
3.注意：每隔 n 天=每（n+1）天。两次相遇之间是过了一个周期。 
4.例 1：小成每 2 天去一次公司，小章每 3 天去一次，1 月 1 日同时出现在
公司，下次同时出现是几月几号？ 
答：问再次相遇，这样的表述就是周期相遇问题。小成每 2 天去一次公司，
小章每 3 天去一次公司，若想撞上，则取最小公倍数 6，每 6 天能见一次，若 1
月 1 号见了，则是每 6 天见了两次，所以只能是 1 月 7 号再见一次。每 6 天用
“过”的思想做。 
5.例 2：小成每隔 2 天去一次公司，小章每隔 3 天去一次，1 月 1 日同时出
现在公司，下次同时出现是几月几号？ 
答：本题和上题的不同点在于“隔”，例如：老师和我去锻炼，我周一到周
五，每一天都去，老师每隔一天去一次，即每隔 1 天和每 2 天是一样的，每隔 n
天=每（n+1）天.

例 3（2018 北京）有一种电子铃，每到整点就响一次铃，每走 9 分钟亮一次 灯。正午 12 点时，它既亮灯又响铃。它下一次既响铃又亮灯是下午几点钟？（ ）
A.1 点钟 B.2 点钟 C.3 点钟 D.4 点钟
【解析】周期相遇问题。先找最小公倍数，60 和 9 的最小公倍数为 180，每 180 分钟相遇一次， 180 分钟是 3 小时，12 点再过 3 小时是 3点钟。【选 C】

【知识点】短周期： 
1.识别：周期较短（一个月左右）。 
2.做法：枚举。

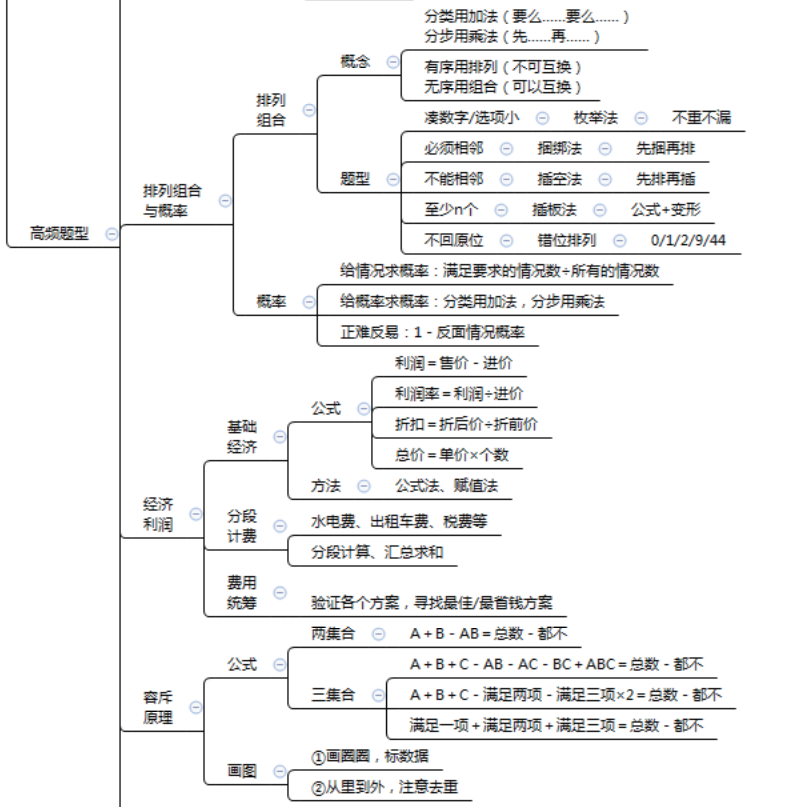
5.排列组合

1.基础题型

1.概述

【知识点】排列组合：两组概念、五种题型。 
1.分类与分步： 
（1）分类（要么……要么……）相加→只会有一种情况发生。 
如：老师从北京去上海玩，可以坐火车，还可以坐飞机去，也可以走着去，要么坐火车，要么坐飞机，要么走路，只能发生一种，用相加，一共有三种情况。 
（2）分步（先……后……）相乘→都发生。 
如：老师到上海后，从上海到广州玩，可以坐飞机，还可以坐火车去，也可以走着去，从北京到上海是三种方式，上海到广州也是三种方式，用乘法，3*3=9 种。 
（3）两者核心区别是：分类只能发生一种，用加法；分步是两者都要发生，用乘法。 
2.排列与组合。 
（1）排列：与顺序有关；组合：与顺序无关。 
例如：从 63 里取 3 个人，有顺序用 A（63,2），没顺序用 C（63,2）。假如三个人去领奖，一等奖一亿，二等奖一万，三等奖一毛，三个人的顺序对结果有影响，与顺序有关用排列（A）。
选出三个人去打扫卫生，谁先谁后无所谓，此时与顺序无关，用组合（C）。 
（2）判定标准：从主体当中任意的挑出两个，调换顺序。对结果有影响，与顺序有关（A）；对结果无影响，与顺序无关（C）。 
3.例 1：从七个葫芦娃中，任选两个一起去救爷爷。 
答：不管选谁都是去救爷爷，顺序对结果无影响，用 C，7 个人中选 2 个为 C（7,2）。 
4.例 2：从七个葫芦娃中，任选两个一起去救爷爷（第一个去探路，第二个去打架）。 
答：有明确分工，顺序有影响，用 A（7,2）。 
4.计算： 
（1）A（7,2）=7*6（从大数开始乘，乘 2 项），A（7,3）=7*6*5（从大数开始乘，乘 3 项），A（10,5）=10*9*8*7*6（从大数开始乘，乘 5 项）。 
（2）C（7,2）=7*6/（2*1），C（7,3）=7*6*5/（3*2*1），C（10,5）=10*9*8*7*6/（5*4*3*2*1）。 
（3）C（7,2）=7*6/（2*1）=21，C（7,5）=7*6*5*4*3/（5*4*3*2*1）=21。C（n,2）=C（n,n-2）， C（7,3）=C（7,4），C（9,7）=C（9,2）。 
（4）A（5,1）=5，C（5,1）=5。A（n,1）=n，C（n,1）=n。 

2.举例

例 1（2018 吉林甲）一位女士为了寻找曾经帮助她的司机，向新闻媒体提供 了她记得的车牌信息。女士看到的车牌号为“吉 AC**”，最后一位是字母，其 他三位全是奇数，且数字逐渐变大，那么符合要求的车牌有（ ）。
A.380 个 B.260 个 C.180 个 D.460 个
10 以内的奇数有 1、3、5、7、9，共 5 种情况，数字要逐渐变大，即三个数字各不相同， 只要选出三个数，顺序直接就固定了，如：（3、5、7）、（5、 7、 9），所以只需把三个数选出来，顺序有且只有一种，为 C（5,3）， C（5,3）26=543/（321）26=1026=260。【选 B】
例 2（2018 浙江）某班共有 8 名战士，现在从中挑出 4 人平均分成两个战斗 小组分别参加射击和格斗考核，问共有多少种不同的方案？（ ）
A.210 B.420 C.630 D.840
【解析】例 2.方法一：8 个人中选 4 个，此时没有分任务，和顺序无关，用C，为 C（8,4）。 4 个人中选 2 人射击，例：选詹姆斯和 REN 去射击，先选谁对结果没有影响，都是去练射击，用 C，为 C（4,2）。 剩下的 2 个人没有选择，只能去格斗，为 C（2,2）。结果为 C（8,4）C（4,2）C（2,2）=（8765/4321）（43/21）1=7061=420。
例 3（2017 吉林）罐中有 12 颗围棋子，其中 8 颗白子，4 颗黑子。从中任 取 3 颗棋子。则至少有一颗黑子的情况有（ ）。
A.98 种 B.164 种 C.132 种 D.102 种
【解析】例 3.方法一：取出 3 颗，至少一颗黑子，可以为 1 黑 2 白、2 黑 1 白、3 黑。 （1）1 黑 2 白：C（4,1）C（8,2）=4（87/2）=112； （2）2 黑 1 白： C（4,2）C（8,1）=43/2*8=48； （3）3 黑：C（4,3）=C（4,1）=4，112+48+4=164。

2.特殊题型

1.概述

1.要相邻（捆绑法）。 
（1）例 1：全排列：李雷、韩梅梅、路人甲、路人乙、路人丙。 
①五个人站一排照相？
答：照相时顺序有关系，有 A（5,5）=5*4*3*2*1=120 种情况。 
②五个人选出三个人站一排照相？ 
答：和顺序有关，有 A（5,3）=5*4*3=60 种情况。也可以先把人挑出来，
再排列，先从 5 个人中挑出 3 个人 C（5,3）， 3 个人 3 个位置全排列 A（3,3），
C（5,3）*A（3,3）=5*4*3/（3*2*1）*3*2=10*6=60。 
例 2：相邻：李雷、韩梅梅、路人甲、路人乙、路人丙，五人站排，李雷和韩梅梅挨着，有几种情况？ 
答：先把李雷和韩梅梅捆一起，要么是李雷在左韩梅梅在右，要么是韩梅梅在左李雷在右，这两人有顺序，用 A（2,2），
把他们看成一个大胖子，大胖子、甲、乙、丙排列，为 A（4,4），先捆再排用乘法，则一共有 A（2,2）*A（4,4）=2*4*3*2*1=48 种情况。 
（2）方法（捆绑法）： 
①先捆，把相邻的捆绑起来，考虑内部顺序。 
②后排，把捆后的“胖子”与其他排列。 
2.不相邻（插空法）。 
3.同素分堆（公式）。 
4.错位排列（结论）。 
5.枚举法。 

2.举例

例 1（2018 联考）两对夫妇各带一个小孩乘坐有 6 个座位的游览车，游览车 每排只有 1 个座位。为安全起见，车的首尾两座一定要坐两位爸爸；两个小孩一 定要排在一起。那么，这 6 人的排座方法有（ ）。
A.12 种 B.24 种 C.36 种 D.48 种
【解析】例 1.“车的首尾两座一定要坐两位爸爸”，即两位爸爸要么一个坐 1、一个坐 6，要么一个坐 6、一个坐 1，有 2 种情况，或者 A（2,2）=2；再排中 间，与两位爸爸无关，不需要再考虑。中间是 4 个人，“两个小孩一定要排在一 起”，先把他们捆起来，即 A（2,2）；捆起来的小孩相当于一个大胖子即一个整 体，再和两位妈妈排在一起，相当于 3 个人，即 A（3,3）。先排两位父亲再捆两 个小孩再排两位母亲，有先有后，分步用乘法，即 2A（2,2）A（3,3）=24，对 应 B 项。【选 B】

【知识点】不相邻： 
1.例：李雷、韩梅梅、路人甲、路人乙、路人丙，五人站排，李雷和韩梅梅不挨着，有几种情况？ 
答：先排甲、乙、丙，三个人排序，即 A（3,3）。三个人形成 4 个空（包括头和尾的空），把李雷和韩梅梅放进这 4 个空中，可以保证李雷和韩梅梅不相邻，
将李雷和韩梅梅放入 4 个空中的 2 个。“李雷在左、韩梅梅在右”和“韩梅梅在左、李雷在右”是不一样的，有顺序，即 A（4,2）。总情况数=A（3,3）*A（4,2）=6*4*3=72。 
2.方法（插空法）： 
（1）先排：将可以相邻的进行排列，排列后形成若干个空位。 
（2）再插：将不相邻的插入到形成的空位中去。 

例 2（2017 联考）某兴趣组有男女生各 5 名，他们都准备了表演节目，现在 需要选出 4 名学生各自表演 1 个节目，这 4 人中既要有男生，也要有女生，且不 能由男生连续表演节目，那么，不同的节目安排有多少种？（ ）
A.3600 B.3000 C.2400 D.1200
【解析】例 2.要选 4 个人，要求既要有男生，也要有女生，先分类讨论：1 个男生、3 个女生；2 个男生、2 个女生；3 个男生、1 个女生。

【知识点】同素分堆（插板法）： 
1.例：7 个相同的苹果分给三个小朋友，每人至少分一个，有多少种分法？ 
答：枚举太费时间，很难保证不出错。分给三个小朋友，即分成三堆，插入两块板子，自然而然把这些苹果分成三堆。左右两边的空位不能放板子，两个板
子不能放在同一个空中，7 个苹果中间有 6 个空，把两块板子放在这 6 个空中，把板子对调，对结果没有影响，用 C，即 C（6,2）=（7-1,3-1）。 
2.方法（插板法）： 
（1）N 个元素有 N-1 个空位，分 M 堆，需要 M-1 个板子。 
（2）至少分一个共有 C（N-1,M-1）方法。 
3.例： 9 个苹果分给 4 个小朋友，每人至少分一个，即（9-1,4-1）=C（8,3）；
20 个苹果分给 5 个小朋友，每人至少分一个，即 C（20-1,5-1）=C（19,4）。

例 3（2016 深圳事业单位）将 9 封相同的信投入 3 个不同的信箱，且每个信 箱至少投入一封信，不同的投法有（ ）种。
A.18 B.21 C.28 D.36 【解析】例 3.插板法，C（n-1,m-1）=C（9-1,3-1）=C（8,2）=87/（21）=28，对应 C 项。【选 C】

【知识点】同素分堆： 
1.例：10 个相同的苹果分给三个小朋友，每人至少分两个，有多少种分法？ 
答：转化的思想，把未知的问题转化为已知的问题。先给每人分一个，还剩10-3=7 个苹果，此时每人还需要至少一个，
即 7 个苹果分给 3 个小朋友，每人至少分一个，C（7-1,3-1）=C（6,2）=6*5/2=15。 
2.例：10 个相同的苹果分给三个小朋友，每人至少分三个，有多少种分法？ 
答：先给每人分两个，转化为每人至少分一个的情况。 
3.例：20 个相同的苹果分给 3 个小朋友，每人至少分 4 个，有多少种分法？ 
答：先每人分 3 个，还剩 20-3*3=11 个苹果。再按照每人至少一个去分，分给 3 个小朋友，即 C（11-1,3-1）=C（10,2）=10*9/2=45 种。 
4.方法（插板法）：
（1）至少 n 个，每人先分（n-1）个。 
（2）剩下的再按照至少分 1 个分，用公式做。

【知识点】错位重排：这个题型自己推导很难，只需要记住结论。 
1.例：你做了一道菜，每个人都不吃自己的，有几种情况？ 
答：自己不能吃自己的，有 0 种情况。 
2.例：你、我都做了一道菜，每个人都不吃自己的，有几种情况？ 
答：两人换着吃，有 1 种情况。 
5.结论：元素个数 1、2、3、4、5、6，对应的错排数 0、1、2、9、44、265。

6.概率问题

1.概述

1.公式：概率=满足/全部。
2.例：3 个绿球、2 个黄球、5 个红球，球都一样，随便摸一个，摸到绿球的概率？ 答：概率=满足/总体，满足情况数是摸到绿球的概率，即 3/（3+2+5） =3/10。 摸到红球的概率为 5/10=1/2。

2.举例

例 1（2018 联考）某单位工会组织桥牌比赛，共有 8 人报名，随机组成 4 队， 每队 2 人。那么，小王和小李恰好被分在同一队的概率是（ ）。
A.1/7 B.1/14 C.1/21 D.1/28
【解析】例 1.概率问题，P=满足的情况数/总情况数，满足情况是“小王和 小李分在同一队”，先把小王随便分到一队，要想满足“小王和小李分在同一队”， 则小王的旁边一定是小李，小王旁边坐小李只有 1 种情况，总情况数是小王旁边 的座位可以坐几个人，剩下 7 人都可以坐，即P=满足的情况数/总的情况数=1/7， 对应 A 项。【选 A】

【知识点】给概率求概率： 
1.例：粉笔征集年会的节目，老师也去参加，得一等奖的概率是 0.1；得二
等奖的概率是 0.2；得三等奖的概率是 0.3。问老师得奖的概率是多少（三个奖
不能同时得）？ 
答：老师要么得一等奖，要么得二等奖，要么得三等奖，分类情况，概率
=0.1+0.2+0.3=0.6。 
2.例：年会之后有抽奖环节，抽到奖的概率是 50%，老师运气比较好，问既
得奖又抽到奖的概率是多少？ 
答：先得奖，后抽到奖，同时发生，分步相乘，概率=0.6*0.5=0.3。 
3.方法：（1）分类加和。（ 2）分步相乘。