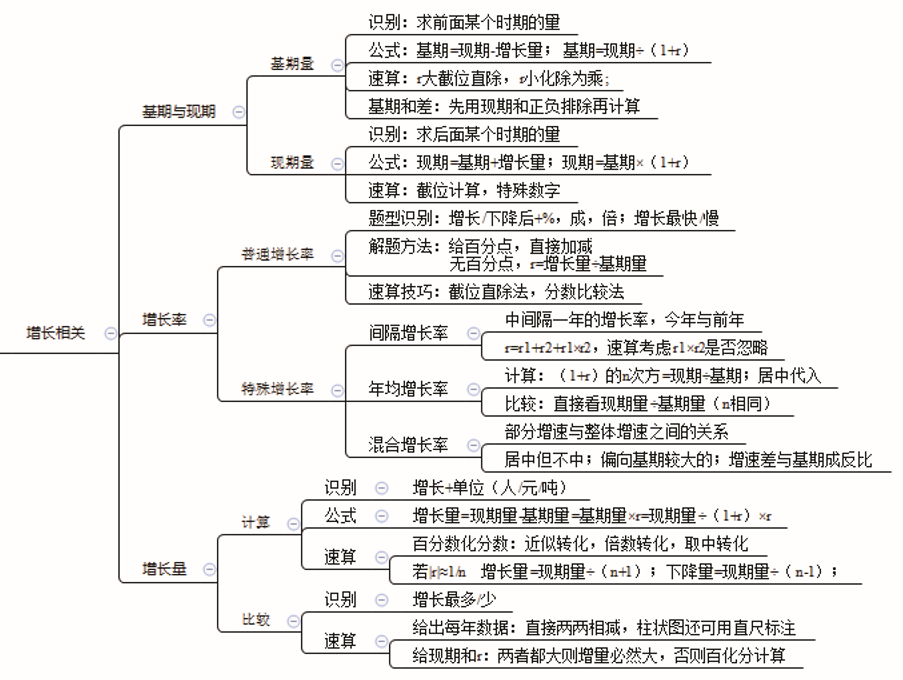
1.思维导图

2.基期和现期

1.概述

（1）作为对比参照的时期称为基期，对应的量称为基期量；而相对于基期 的为现期，所对应的量称为现期量。
（2）考试的时候，总是用过去和现在比，用现在和未来比，因此可以记为： 时间靠前的是基期，时间靠后的是现期。比如 2016 年比 2015 年……，这里 2015 年时间靠前是基期，对应量是基期量，2016 年时间靠后，是现期，所对应量是 现期量。
（3）没有时间的：“比”之后的为基期。比如小明的身高比小红高 10cm， 这里没有时间，“比”之后，小红的身高是基期，所对应量是基期量。

2.基期

考查形式：
（1）给现期量和增长量：基期量=现期量-增长量。
（2）给现期量和增长率：基期量=现期量/（1+r）。
2016 年末全国共有艺术表演团体 12301 个，比上年末增加 1514 个，从业人 员 33.27 万人，增加 3.08 万人。其中各级文化部门所属的艺术表演团体 2031 个，占 16.5%；从业人员 11.52 万人，占 34.6%。
例 1（2018 联考）2015 年末，全国拥有艺术表演团体的数量是（ ）。
A.10787 个 B.12301 个 C.14237 个 D.22031 个
【解析】基期量=现期量-增长量=12301-1514，看选项， B 项就是 12301，结果是 12301 减一个正数，答案一定比 12301 小，只有 A 项符合。【选 A】
2016 年，规模以上工业企业实现利润 1549.3 亿元，比上年下降 0.7%。重点 行业中，电力、热力生产和供应业实现利润 490.1 亿元，下降 7.7%；汽车制造 业实现利润367.8亿元，增长5.4%；医药制造业实现利润150.7亿元，增长15.3%； 计算机、通信和其他电子设备制造业实现利润 84.8 亿元，增长 36.8%；专用设 备制造业实现利润 73.9 亿元，增长 70.3%。
例 2（2018 北京）2015 年该市规模以上专用设备制造业约实现利润多少亿 元？（ ）
A.22 B.33 C.43 D.55
【解析】基期=现期/（1+r）=73.9/1.703，选项首位不同，分母截 2 位计算，73.9/17，首位商 4，对应 C 项。【选 C】 【注意】看选项，首位不同截 2 位计算。

【知识点】化除为乘： 
1.应用条件：求基期量，|r|≤5%，选项差距小（往往是第三位不同）。 
2.应用方法：A/（1+r）≈A*（1-r）=A-A*r（相对误差为 r²）。 
3.推导：A/（1+r）=A*（1-r）/[（1+r）*（1-r）]=A*（1-r）/（1-r2）=A*
（1-r）/1=A-A*r。 
①|r|≤5%，r²≤（5%）²=万分之 25=千分之 2.5=0.25%，误差很小，可以忽
略。 
②初一时学的平方差公式：（a+b）*（a-b）=a²-b²。 
4.知道推导过程，就知道误差范围，可以根据选项来推断能不能用化除为乘。
【补例】238.7/（1-2.2%）=（  ） 
A.249.4 B.236.5 C.240.1 D.244.1 
【解析】补例.|r|＜5%，选项差距小，可以化除为乘。238.7/（1-2.2%）≈
238.7*（1+2.2%）≈238.7+5+≈243.7+，对应 D 项。【选 D】 

【知识点】同比与环比（同比看年，环比看尾）： 
1.同比：与历史同期相比较，往往指去年同期。比如 2018 年同比就是和 2017
年比，2018 年 8 月同比是和 2017 年 8 月比，2018 年 8 月 1 号同比是和 2017 年
8 月 1 号比。 
2.环比：环比实际上是指“与紧紧相邻的上个统计周期相比较”，包括日环
比、月环比、年环比等。环比看的是“尾”，“尾”即最小单位。比如 2018 年环
比是和 2017 年比，2018 年 8 月环比是和 2018 年 7 月比，2018 年 8 月 1 号环比
是和 2018 年 7 月 31 号比。 
3.同比就是看去年，环比就是看末尾的单位，向上数一个最小单位。

【知识点】拓展术语： 
1.顺差：顺差又称出超，可以简单记忆为出口额超过进口额。 
2.逆差：逆差又称入超。入就是进，进超过了出，就是逆差。 

【知识点】普通基期量比较：   
1.本质：分数比较。绝大多数是给现期量和 r 来比较，基期=现期/（1+r），
是一个分数，因此是分数的比较。   
2.方法：比最大，先找分子大分母小的；比最小，先找分子小分母大的。
3.分数比较时尽量根据选项比较，可以节省计算量。

3.现期

考查形式：
（1）给基期量和增长量：现期量=基期量+增长量。
（2）给基期量和增长率：现期量=基期量*（1+r）。
（3）速算技巧：截位计算，特殊数字（比如 9.64%近似看作 10%=1/10）。

3.增长率

1.基本术语

增长率：：增长率表述两者变化的相对量，一般是用 r 表示， r=增长量/基期量。增长率又称增速（增长速度）、增幅或者增长幅度、增值率等， 增长率为负时表示下降，下降率也可直接写成负的增长率，负的增长率叫降幅， 比如-5%=降幅 5%。
1.百分数
（1）百分数表示两个量的比例关系，用除法计算。 （2）例子：2017 年某地区小麦产量为 60 万吨，总体粮食产量为 100 万吨， 则 2017 年该地区小麦产量占粮食产量的比重为？
答：小麦产量/粮食产量=60/100=60%。
2.百分点
（1）百分点表示百分数的变化，用加减法计算。
（2）例子：2017 年某地区小麦产量同比增长率为 8%，较玉米产量的增长率 低了 5 个百分点，则 2017 年该地区玉米产量的增长率为？
答：小麦产量的增长率 8%比玉米的低，则玉米的增长率高，出现了“百分 点”，做加减法，玉米的增长率为 8%+5%=13%。看到百分点，做的运算是加减法。
3.增长率与倍数的辨析
1.概念：
（1）增长率指比基数多出的比率，倍数指两数的直接比值。
（2）例子：2016 年小刘每月零花钱为 100 元，2017 年小刘每月零花钱为 300 元。
①小刘 2017 年每月零花钱是 2016 年的多少倍？答：A/B=300/100=3 倍。 ②小刘 2017 年每月零花钱比 2016 年增长了（多了）多少倍？答：出现了“增 长了/多了”，问的是增长率，r=（300-100）/100=2 倍。
2.倍数=增长率+1。

【知识点】成数与翻番的辨析：   
1.成数：几成相当于十分之几，比如两成=20%。   
2.翻番：翻一番为原来的 2倍；翻两番为原来的 2²=4 倍；依此类推，翻 n
番为原来的 2的n次方倍。

2.普通增长率

考查形式：
（1）给百分点：直接加减。
（2）无百分点：r=增长量/基期量。
2013 年全国水稻种植面积达 4.55 亿亩，比上年增加 260 多万亩。但由于强 降雨及洪涝灾害，总产量较上年减少 62 万吨，总产量为 20361 万吨。
例 4（2016 上海）2013 年我国水稻种植面积比 2012 年增长约（ ）。
A.5.75% B.5.75‰ C.2.75% D.2.75‰ 【解析】例 4.增长+%/‰，r=增长量/基期量，选项存在 10 倍的关系，保留单 位计算，增长量/基期量≈260 万/（4.55 亿-260 万），一亿=一万万，原式≈260/（45500-260）=260/45200+=2.6/452+，4.52/452=1%， 则 2.6/452＜4.52/452=1%，排除 A、C 项，首位商 5，对应 B 项。【选 B】 注意：当选项之间存在十倍、百倍、千倍的关系的时候，要结合单位进行计算

【知识点】普通增长率的比较：   
1.题型识别：增长最快/慢。   
2.公式：r=增长量/基期量=（现期量- 基期量） /基期量=现期量/基期量-1。   
3.比较方式：   
（1）给增长量：增长量/基期量。   
（2）给现期量和基期量：   
①如果现期量/基期量≥2（倍数关系明显），直接比较“现期量/基期量”大小，
所有增长率列式中都有“-1”，就不带“-1”比较，直接比较“现期量/基期量” 。   
②如果现期量/基期量＜2，直接比较“增长量/基期量”大小。

3.特殊增长率 （广东省考）

1.间隔增长率（★★）：考得最多。
2.年均增长率：考得最少，三四年考一次。
3.混合增长率（★）：考的频率次于间隔增长率。间隔增长率和混合增长率 每年考 1～2 题，有时候考间隔增长率，有时候考混合增长率，有时候都考。

【知识点】间隔增长率
1.题型识别：中间隔一年，求增长率/倍数/基期量。 
2.公式：r 间=r1+r2+r1×r2；间隔倍数=r 间+1；基期量=现期量/（1+r 间）。  
3.速算技巧：  
（1）结合选项排除（例 3）。   
（2）r1、r2的绝对值均小于 10%，r1×r2可以忽略。   
（3）特殊分数。比如 10%=1/10，20%=1/5。

1.例子：
（1）已知：某企业 2015 年主营业务收入相对于 2014 年的增长率为 r1，2016 年相对于 2015 年的增长率为 r2。求：该企业 2016 年主营业务收入相对于 2014 年的增长率为多少？
（2）识别：2016 年和 2014 年中间间隔一年，间隔了 2015 年，求的是增长 率，则考的是间隔增长率。
2.推导：如果 2014 年为 M，2015 年比 2014 年的增长率为 r1，则 2015 年为 M（1+r1）， 2016 年比 2015 年的增长率为 r2，则 2016 年为 M（1+r1）×（1+r2）， r= （ 2016 年 -2014 年）/2014 年 =[M× （ 1+r1 ） × （ 1+r2 ） -M]/M=1+r1+r2+r1×r2-1=r1+r2+r1×r2。
3.题型识别：中间隔一年，求增长率。
4.公式：r=r1+r2+r1×r2。有点像高利贷（利加利、利滚利）。
例1：2016 年 1～4 月份，我国全社会用电量 18093 亿千瓦时，同比增长 2.9%。从 不同产业看，第一产业用电量 270 亿千瓦时，同比增长 9.1%；第二产业用电量 12595 亿千瓦时，同比增长 0.2%；第三产业用电量 2516 亿千瓦时，同比增长 10.0%， 增速比上年同期提高 2.1 个百分点；城乡居民生活用电量 2711 亿千瓦时，同比 增长 9.5%，增速比上年同期提高 5.4 个百分点。
例 1（2017 山东）与 2014 年同期相比，2016 年 1～4 月份第三产业用电量 上升了约（ ）。
A.15% B.19% C.23% D.27%
【解析】2016 年比 2014 年，中间间隔一年，求增长率，是求间隔增长 率。2016 年比 2015 年的增长率为 10%，增速比上年同期（2015 年）提高 2.1 个 百分点，高减低加，则 2015 年的增长率为 10%-2.1%=7.9%，即 2015 年比 2014 年的增长率为 7.9%。r=r1+r2+r1×r2=7.9%+10%+7.9%×10%≈17.9%+8%×1/10=17.9%+ 0.8%=18.7%≈19%。【选 B】
已知：某企业 2016 年主营业务收入为 A，2015 年相对于 2014 年的增长率为 r1，2016 年相对于 2015 年的增长率为 r2。求该企业 2014 年的主营业务收入是多 少？
答：2016 年与 2014 年中间间隔一年，求的是主营业务收入，是一个具体量， 2014 年为基期，即求基期量。已知基期=现期/（1+r）， 同理，间隔基期=现期/ （1+r 间），r 间=r1+r2+r1×r2，求出 r 间，代入计算即可。

【知识点】年均增长率：**（广东省考得比较少，国考中也考得较少，考得相
对多的是比较类的题目）   
1.题型识别  ： 
（1）比较类：年均增长（增速）最快/排序。  
（2）计算类：年均增长率为……。

例2：某企业 2010 年的收入为 100 亿元，2015 年的收入为 200 亿元，则 该企业 2010 年至 2015 年收入的年均增长率为多少？
答：“均”说明相等，年均增长率指的是每年的增长率都相等。2010 年的收 入为 100，年均增长率用 r 表示，则 2011 年的量为 100×（1+r），2012 年的量为 100×（1+r）²，2010 年到 2011 年增长 1 年，是 1 次幂，2010 年到 2012 年增长 2 年，是 2 次幂，则 2010 年到 2015 年增长了 5 年，应该是 5 次幂，200=100×（1 +r）^5。200 是现期量，100 是基期量，现期量=基期量×（1+r 年）^n。
3.年均增长率的比较：
（1）公式：基期量*（1+r 年）^n=现期量→（1+r 年）^n=现期量/基期量（n 为 现期和基期的年份差）。
（2）比较技巧：如果 n 相同，直接比较“现期量/基期量”。

【知识点】混合增长率：
1.题型识别：部分增速与整体增速之间的关系。   
（1）房产、地产→房地产。后面是整体，前面两者是部分。   
（2）进口、出口→进出口。   
（3）城镇、农村→全国。   
2.判断口诀：广东比较常考前两个。   
（1）居中但不中（整体增长率介于部分增长率之间）;
（2）偏向基期较大的（做题中一般用现期量近似代替）;

（1）居中但不中 例：咱班男同学消费的同比增速为 10%，女同学的同比增速为 50%。问：全 班同学消费的同比增速在什么范围？
答：男同学是一部分，女同学是另一部分，合起来是全班的，总体的增长率 一定在 10%～50%之间，可类比溶液问题。
（2）偏向基期较大的
例：咱班男同学的消费总计为 1 万元，同比增速为 10%，女同学的消费总计 为 5000 元，同比增速为 50%。
问：全班同学消费的同比增速约是？
A.8% B.21% C.49% D.52%
答：画图理解，男同学在左边，为 10%，女同学在右边，为 50%，总体的增 长率在 10%～50%之间，排除 A、D 项。正中间是（10%+50%）/2=30%，因为男、女同学 的基数不一样，男同学基数大，所以不正好是 30%，总体应该在 10%～30%之间，排除 C 项，对应 B 项。【选 B】

4.增长量

1.概述

1.题型识别：增长+具体单位（人/元/吨）。看到增长+%/成/倍，是考查增长率。
2.公式：增长量=现期量- 基期量（基本公式）=基期量×r=现期量÷(1+r)×r。
（1）现期量=基期量×（1+r），所以增长量=基期量×（1+r）- 基期量=基期量×r。
（2）基期量=现期量÷（1+r），所以增长量=现期量÷（1+r）×r。
3.考查形式：
（1）给现期量、基期量：增长量=现期量- 基期量。
（2）给现期量、r：增长量=现期量÷（1+r）×r。

2. 年均增长量

1.题型识别：年均（平均每年）+增长+单位。
2.示例：2012 年小刘每月零花钱为 50 元，2017 年小刘每月零花钱为 150 元，则 2012～2017 年间，小刘每月零花钱的年均增长量为多少元钱？
答：求年均增长量，“均”说明相等，“年均”则说明每年都相等。设年均 增长量是 x，2012 年：50；2013 年：50+x；2014 年：50+2x……2017 年：50+ （2017-2012）x=50+5x。现期量=基期量+n*年均增长量，n 代表年份差，即年均 增长量=（现期量- 基期量）÷n。
3.公式：年均增长量=（现期量- 基期量）÷年份差。
4.年均增长类问题年份差的确定:
（1）一般情况（除江苏外）：2011 年～2015 年：年份差为 4（2015-2011=4）， 基期为 2011 年，现期为 2015 年。
（2）五年规划（全国都一样）：“十二五”期间（2011～2015 年）：年份差 为 5（基期往前推一年，2015-2010=5），基期为 2010 年，现期为 2015 年.
5.举例
2015 年末该市拥有技术企业 3478 家，人才总数由 2010 年末的 146 万人增 加到 2015 年末的 227 万人。其中，高层次人才由 2010 年末的 8 万人增加到 2015 年末的 18 万人。每万名劳动者中研发人员由 158 人增加到 175 人。 例 3（2017 江苏）“十二五”期间（2011～2015 年），该市人才总数年平均 增加人数是（ ）。
A.13.6 万人 B.14.2 万人 C.15.6 万人 D.16.2 万人
【解析】例 3.“十二五”期间，基期是 2010 年，现期是2015 年，找到“人才”（不是“高层次人才”），列式子， （现期量- 基期量）/年份差=（227-146）/5=81/5=16+，对应 D 项。【选 D】

3.已知现期量、r 求增长量。

1.公式：增长量=现期÷(1+r)×r 。增长（r 为正）、减少（r为负）。
2.示例：2015 年小刘每月的零花钱为 70 元，同比增长率为 16.7%，则小刘 2015 年每月的零花钱比 2014 年约增长了多少钱？
A.5 元 B.10 元 C.15 元 D.20 元
答：给增长+具体数值，考查增长量，已知现期和 r。列式子 增长量=现期量/（1+r）r=70/（1+16.7%）16.7% 对应 B 项。

常考特殊分数： 
（1）1/2 家族：1/2=50%，1/4=1/2 的一半=50%/2=25%，1/8=1/4 的一半=25%/2=12.5%，1/16=6.25%。 
（2）1/3 家族：1/3≈33.3%，1/6=1/3 的一半≈16.7%，1/12=1/6的一半≈8.3%。 
（3）1/5 家族：1/5=20%，1/10=1/5 的一半=10%，1/20=1/10 的一半=5%。 
（4）1/7 家族：7*14=98，1/7≈14.3%，1/14=1/7 的一半7.1%。 
（5）1/9 家族：9*11=99，1/9≈11.1%，1/11≈9.1%。 
（6）单独记忆：1/13≈7.7%，1/15≈1/5÷3≈6.7%。 
（7）1/17≈5.9%，1/18≈5.6%，1/19≈5.3%，利用尾数 3、6、9（倒序）来记忆，考查较少

4.比较 概述

【知识点】增长量比较：
1.题型识别：增长最多/少，指的是量。如果问增长快/慢，指的是增速，即增 长率。
2.考查形式：
（1）给现期和基期（直接减，考查少）：增长量=现期量- 基期量。
（2）给现期、r（每年都会考查一道，不是计算类就是比较类）：
①大大则大。
②百化分计算。

5.给现期量、r，比较增长量大小

大大则大：
（1）现期量大，同时 r（正值）也大，则其增长量大。
（2）现期量大，同时|r|（负值）也大，则其减少量大。
举例：
（1）2017 年，小马有 200 亿，同比增长 25%，小刘有 110 亿，同比增长 10%， 则 2017 年谁的增长量大？
答：小马现期本来就大，增长率也大，则大大则大，小马增长量一定大。
（2）2017 年，小马有 200 亿，同比下降 25%，小刘有 110 亿，同比下降 10%， 则 2017 年谁的减少量大？
答：减少量则增长率是负的，小马现期量大，增长率的绝对值大，则减少量 一定大。
（3）2017 年，小马有 200 亿，同比增长 25%，小刘有 110 亿，同比增长 50%， 则 2017 年谁的增长量大？
答：小马现期量大，小刘增长率大，一大一小可以利用百化分计算。r 小马 =25%=1/4， r 小刘=50%=1/2，则小马增长量=200/（4+1）=40，小刘增长量=110/（2+1） =30+＜40，即小马增长量＞小刘增长量。

比重：
国考一般考查 4～6 道
2018年国考中考查了 8 道。

6.比重-现期比重

现期比重：比重指部分在总体中占的比率。
2.公式：比重=部分/总体。
3.考查形式：
（1）已知部分和总体，求比重。比重=部分/总体。
（2）已知部分和比重，求总体。总体=部分/比重。
（3）已知总体和比重，求部分。部分=总体*比重。
4.比重的特殊表述形式： （1）增长贡献率：增长贡献率指部分增量在总体增量中所占的比例，即增长贡献率=部分增量/总体增量。
（2）利润率：
①区分：在资料分析中，利润率考查的都是销售利润率（或者收入利润率）， 利润率=利润/收入；在数量关系中，利润率考查的都是成本利润率，利润率=利 润/成本。
②示例：2017 年某企业实现主营业务收入 100 亿元，利润总额为 10 亿元， 则期营业利润率为 10%。利润率=利润/收入=10/100=10%。
例 4：2017 年上半年， S 市出口手机 1.9 亿台，比去年同期减少 22.7%；价值 513.1 亿元人民币，下降 23.7%。6 月份当月出口 3217.5 万台，减少 23.7%；价值 86 亿元，下降 27.8%。上半年， S 市出口 GSM 数字式手机 8910.5 万台，减少 20.5%； 出口含 4G 手机在内的其他手机 7480.6 万台，减少 26.1%；出口 CDMA 数字式手 机 307.3 万台，减少 19.2%。
2017 年上半年，S 市出口 GSM 数字式手机占同期手机出口 总量的比重，约比出口含 4G 手机在内的其他手机占同期手机出口总量比重高（ ） 个百分点。
A.1.9 B.3.8 C.7.5 D.13.6
【解析】例 4.问题时间和材料时间相同，求现期。问的是比重，为现期比 重问题。本题实际上是两个比重进行做差，定位材料，GSM 的比重为 8910.5 万 /19000 万；4G 手机的比重为 7480.6 万/19000 万；做差=8910.5 万/19000 万 -7480.6 万/19000 万=1400+万/19000 万＜10%，排除 D 项；直接除，首位商 7+， 对应 C 项。【选 C】
例 7：从全国园林水果种植面积的地区分布情况看，在主要大宗果品中，苹果“十 二五”期初种植面积 214 万公顷，期末 232.8 万公顷，增长 8.8%；柑橘期初种 植面积 221.1 万公顷，期末 251.3 万公顷，增长 13.7%；梨期初种植面积 106.3 万公顷，期末 112.4 万公顷，增长 5.7%；葡萄期初种植面积 55.2 万公顷，期末 79.9 万公顷，增长 44.7%；香蕉期初种植面积 35.7 万公顷，期末 40.9 万公顷， 增长 14.6%。
对“十二五”期间水果种植面积增长贡献最大的果品是（ ）。
A.苹果 B.柑橘 C.梨 D.香蕉
【解析】例 7.问“增长贡献”，即考查增长贡献率，求最大，增长贡献率= 部分增量/总的增量。本题总的增量是一样，只需要找部分增量最大即可。依题 意得，苹果的增量：232.8-214=18+；柑橘的增量：251.3-221.1=30+；梨的增量： 112.4-106.3=6+；香蕉的增量：40.9-35.7=5+，明显是柑橘的增长贡献率最大， 对应 B 项。【选 B】

7.比重-基期比重

1.题型识别：问题时间在材料之前，占，比重。
2.（1）示例：2017 年小麦产量为 A 万吨，同比增长率为 a，2017 年粮食 产量为 B 万吨，同比增长率为 b，则 2016 年小麦产量占粮食产量的比重为多 少？
（2）推导：2016 年小麦/2016 年粮食=A/（1+a）÷[B/（1+b）]=A/（1+a）×[（1+b）/B]=A/B×[（1+b）/（1+a）]。
3.公式：A/B×[（1+b）/（1+a）]。
A：分子（部分的现期）；B：分母（总体的现期）；a：分子（部分）的增 长率；b：分母（总体）的增长率。
4.速算：
（1）截位直除。
（2）先算现期比重（即 A/B，考试往往会挖现期比重坑），再看（1+b）/（1+a） 大于 1 或小于 1 结合选项排除答案。
例 ：2016 年，中小企业实现利润总额 4.3 万亿元，同比增长 6.2%，增速比上年 提高 2.0 个百分点，其中，中型企业利润总额 1.8 万亿元，同比增长 6.4%，小 型企业利润总额 2.5 万亿元，同比增长 6.1%。
2015 年中小企业利润总额中，中型企业利润所占比重约 为（ ）。
A.41.7% B.41.9% C.58.1% D.58.3%
【解析】问题时间为 2015 年，材料时间为 2016 年，求基期。出现“占…… 比重”，求比重，判定题型为基期比重问题。基期比重公式=A/B[（1+b）/（1+a）]， 定位材料，代入数据得=1.8/4.3[（1+6.2%）/（1+6.4%）]。先算现期比 重：1.8/4.3≈0.419=41.9%；再看（1+b）/（1+a）：（1+6.2%）/（1+6.4%）＜1， 乘积比 41.9%小，排除 C、D 项；发现 B 项是现期的坑，排除 B 项，对应 A 项。【选 A】
【注意】先算现期比重，再看（1+b）/（1+a）大于 1 或小于 1 结合选项排除答案。

8.比重-两期比重

【知识点】两期比重比较——升降：
1.题型识别：两个年份，一个比重。
2.（1）示例：2017 年小麦产量为 A 万吨，同比增长率为 a，2017 年粮食 产量为 B 万吨，同比增长率为 b，则 2017 年小麦产量占粮食产量的比重相对 于去年上升还是下降？
（2）推导：现期比重- 基期比重=A/B-A/B×[（1+b）/（1+a）]=A/B×[1 （1+b）/（1+a）]=A/B×[（1+a）/（1+a）-（1+b）/（1+a）]=A/B×[（a-b）/ （1+a）]。
3.（1）公式：现期比重- 基期比重=A/B-A/B×[（1+b） / （1+a） ]=A/B×[（a-b） /（1+a）]。
（2）A/B 是现期比重，是正数；1+a 也是正数，因为分子增长率低于100%， 即 a＞-100%=-1，所以 1+a＞0。例如：经济增长率是不可能下滑 100%的。
4.升降判定：a 为分子（部分）的增长率；b 为分母（总体）的增长率。
（1）a＞b，比重上升。
（2）a＜b，比重下降。
（3）a=b，比重不变。
5.注：比较时带着正负号进行比较。例：a=3%＞b=-5%。
例：2015 年江西省规模以上工业企业实现主营业务收入 32459.4 亿元，比上年 增长 4.3%；实现利税总额 3543.8 亿元，增长 3.8%，其中，利润总额 2128.0 亿 元，增长 2.4%，主营业务收入超百亿元的企业 10 户，其中，江铜集团 2010.4 亿元，居全省首位。
2015 年江西省规模以上工业企业的营业利润率与上年同期相比（ ）。
A.有所上升 B.有所下降 C.持平 D.无法判断
【解析】例 1.问题时间与材料时间相同，求现期；在资料分析中，利润率= 利润/主营业收入（相当于比重），定位材料，利润对应 a=2.4%，主营业收入对 应 b=4.3%，a＜b，比重下降，对应 B 项。【选 B】
【知识点】两期比重比较：上升、下降多少个百分点。
1.示例：2017 年小麦产量为 A 万吨，同比增长率为 a，2017 年粮食产量为 B 万吨，同比增长率为 b，则 2017 年小麦产量占粮食产量的比重相对于去年上升、 下降多少个百分点？
2.（1）公式：现期比重- 基期比重=A/B*[（a-b）/（1+a）]=A/B×[1/（1+a）]× （a-b）＜|a-b|。
（2）推导：现期比重=A/B＜1，如果 a＞0，则 1+a＞1，推出 1/（1+a）＜1； 如果 a＜0，则 1+a＜1，推出 1/（1+a）＞1。一般情况下，A/B 往往比 1 小的多， 假如 a=-20%，1/（1-20%）=1/0.8=1.25，乘积一定是＜1。
（3）在国考中，A/B×[1/（1+a）]一般都是＜1。
3.方法：
（1）判方向（a＞b，上升，a＜b，下降）。
（2）定大小：两期比重差＜|a-b|。绝大部分的情况是＜|a-b|的选项只有一个。
例：2016 年，J 省规模以上工业取水量为 86.4 亿立方米，比上年增长 4.4%。其 中，直接采自江、河、淡水湖、水库等的地表淡水 68.1 亿立方米，比上年增长 3.8%，所占比重比上年下降 0.4 个百分点；自来水取水量 15.9 亿立方米，同比 增长 6.0%。 J 省 2016 年规模以上工业自来水取水量占总取水量的比 重比上年（ ）。
A.提高 0.3 个百分点 B.下降 0.3 个百分点 C.提高 4 个百分点 D.下降 4 个百分点
【解析】例 4.出现两个时间+比重，为两期比重比较问题。（1）判方向：工 业自来水对应 a=6.0%，总取水量对应 b=4.4%，a＞b，比重上升，排除 B、D 项； （2）定大小：结果要＜|a-b|=|6%-4.4%|=1.6%，小于 1.6 个百分点，排除 C 项， 对应 A 项。【选 A】

8.线段法

` 线段法:距离与量成反比。 `
1.引例：浓度为 10%的 A 溶液 m 克与浓度为 20%的 B 溶液 n 克进行混合，混 合后的浓度为 14%，求 m：n？
答：基本公式为溶质=溶液×浓度。A 溶液溶质为 10%×m，B 溶液溶质为 20%× n，则 10%×m+20%×n=14%×（m+n）， 化简得（20%-14%）×n=（14%-10%）×m，m/n= （20%-14%）/（14%-10%）=6/4=3/2。
2.线段法：
（1）混合之前写两边，混合之后写中间，距离与量成反比。
（2）左边是 m，浓度为 10%，右边是 n，浓度为 20%，混合后的浓度 14%在 中间。距离之比（14%-10%）：（ 20%-14%）=2：3，量之比 m：n=3：2。