1.思维导图
2.基础数列
1.概述
【知识点】基础数列:基础数列是数字推理的地基,很多其他数列通过加减运算回归到基础数列;广东省考中甚至会直接考查基础数列。
1.等差数列:1、6、11、16、21、26,公差为 5 的等差数列。
2.等比数列:3、6、12、24、48、96,公比为 2 的等比数列。
3.质数数列:广东省考特别爱考质数数列,质数就是除了 1 和它本身没有其它约数的数,例如:2、3、5、7、11、13、17、19。
4.合数数列:了解即可,考查不是很多;不是质数的数就是合数,例如:4、6、8、9、10、12。特殊说明:1 既不是质数,又不是合数。
5.周期数列:
(1)数字循环:1、5、1、5、1、5;5、2、0、5、2、0、5、2、0,数字周期出现。
(2)符号循环:+1、-2、+3、-4、+5,符号正负交替出现,下一项应为-6。
6.简单递推数列:
(1)递推和:1、2、3、5、8、13。
(2)递推差:21、13、8、5、3、2。
(3)递推积:1、2、2、4、8、32。
(4)递推商:256、32、8、4、2、2。
2.例子
例1(2015广东)19,38,57,76,95,( )
A.114 B.133 C.171 D.190
【解析】例1.观察数列,后一项-前一项=19,构成公差为19的等差数列,则( )=95+19=114,对应A项。【选A】
例2(2014广东)4,12,36,108,( )
A.223 B.257 C.315 D.324
【解析】例2.观察数列,后一项/前一项=3,构成公比为3的等比数列,则( )=108*3=324,对应D项。【选D】
例3(2018广州)2,3,-1,4,-5,( )
A.-8 B.-9 C.8 D.9
【解析】例 3.观察数列,发现:2-3=-1,3-(-1)=4,( -1)-4=-5,构成
递推差数列,则( )=4-(-5)=9,对应 D 项。【选 D】
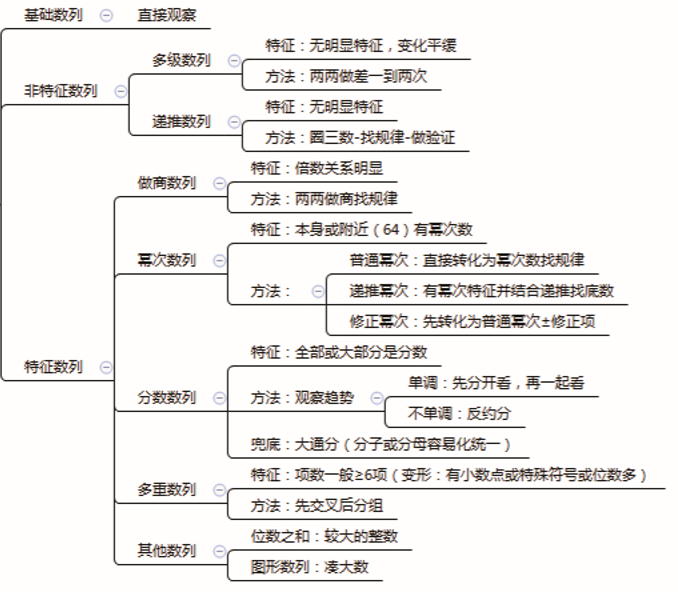
3.多级数列
1.概述
1.题型特征:无明显特征,变化趋势平缓。
2.解题方法:两两做差,一次不行做两次。
3.注意:
(1)做差时保持方向一致,要么后减前,要么前减后。
(2)做差的目的是将数列转化为基础数列。
(3)有根号:转化为纯数字。
(4)差值为新数列:有规律直接做,无规律再做差。
2.列子
例1(2018广州)2,8,18,32,50,( )
A.68 B.72 C.76 D.98
【解析】例1.观察数列,没有明显特征,考虑做差,做差得:6、10、14、18,做差后构成公差为4的等差数列,做差后的数列下一项应为22,则原数列( )-22=50,所以( )=72,对应B项。【选B】
例3(2018广州)1,4,10,22,46,( )
A.70 B.72 C.92 D.94
【解析】例3.观察数列,没有明显特征,考虑做差,做差得:3、6、12、24,做差后构成公比为2的等比数列,
做差后的数列下一项应为48,则( )-46=48,所以( )=94,对应D项。【选D】
例5(2018江苏)1,3,6,11,18,( )
A.25 B.27 C.29 D.33
【解析】例5.观察数列,没有明显特征,考虑做差,做差得:2、3、5、7,做差后构成质数列,做差后的数列下一项应该是11,
则( )-18=11,所以( )=29,对应C项。【选C】
例6(2018广州)5,7,17,19,29,( )
A.31 B.39 C.41 D.47
【解析】例6.观察数列,没有明显特征,考虑做差,做差得:2、10、2、10,做差后构成周期数列,做差后数列的下一项是2,
则( )-2=29,所以( )=31,对应A项。【选A】
例 8(2016 吉林甲) √2, √6,( ), 2√5, √30
A. √7 B. 3√2 C. √10 D. 2√3
【解析】例 8.数字推理的重点看的是“数”,本题的“ √”是用来迷惑考生的。 2√5和数列中其他数字的形式不一样,要统一形式,将数字放在根号内;
统一后得到 √2, √6( )、 √20, √30 ,单独看根号下的数字:2,6,( ), 20,30,做差得:4、?、?10。出现两个“?”,考试中可以代入选项依次进行验证,
也可以大胆猜测,猜测做差后数列为:4、6、8、10;验证:6+6=12,12+8=20,符合规律,则原数列( )= =2 ,对应 D 项。【选 D】
例 9(2016 江苏)2,3,4,3√3 ,√46( )
A.81 B. 2√5 C. 3√5 D.9
【解析】例 9.将数列中数字还原至根号下,得: √4、 √9、 √16、 √27、 √46,单独看根号下的数字:4,9,16,27,46,做差得:5,7,11,19,依旧没有规
律,尝试再次做差,得:2,4,8,则二次做差后的下一项应为 16,所以一次做差后的数字应为 35,原数列( )=√(35+46) =√81 =9,对应 D 项。【选 D】
4.递推数列
1.概述
1.题型特征:没有明显特征,排在多级之后。
2.解题方法:
(1)简单递推直接做。如:例 1、例 2。
(2)圈仨数——凑大数——做验证。
如:例 3、例 4、老师编写的引例考查乘法;例 5、例 8 考查两项之间的倍
数关系;例 6、例 7 的变化趋势慢,考查加减;例 9 的变化趋势快,考查平方。
3.注意点:
(1)圈仨数——不大不小。
(2)一一对应做验证。
2.例子
例1(2018浙江)10,12,13,22,25,35,( )
A.60 B.50 C.47 D.37
【解析】例1.观察数列,数列的变化趋势不是很快,做和可以发现:10+12=22,
12+13=25,13+22=35,发现做和后的结果等于原数列相隔的一项,则( )=22+25=47,对应C项。【选C】
例2(2018吉林)2,3,6,18,( ),1944
A.102 B.96 C.58 D.108
观察数列,优先考虑做差,做差没有明显规律;发现数列从较小的数字跳跃到1944,变化趋势非常快,
此时优先考虑乘法;发现:23=6,36=18,618=108,符合递推积规律,则18( )=1944,所以( )=1944/18=108,
对应D项。【选D】
4.例.2,3,5,14,69,( )
A.968 B.967 C.966 D.965
【解析】例.做差后没有明显规律,考虑递推数列。若圈三个大的数,比较
难计算;若圈最小的三个数,小的数字规律多,非常容易出现混乱;因此,优先
圈中间的三个数:3,5,14。发现数列变化较快,优先考虑乘法,发现35-1=14;
验证规律:23-1=5,514-1=69,“ -1”称为修正项,则1469-1=( ),所以( )
=966-1=965;也可以结合尾数法,尾数为6-尾数为1的结果尾数应为5,对应D项。
【选D】
例3(2016深圳)2,2,3,4,8,24,( )
A.160 B.176 C.192 D.256
【解析】例3.观察数列,做差得:0、1、1、4、16,没有明显规律,考虑递
推。圈中间3、4、8这三个数,结合选项,出现三位数,数字变化趋势快,优先
考虑乘法,发现:34-4=8;验证:22-1=3,23-2=4,48-8=24,发现修正项
为:-1、-2、-4、-8构成公比为2的等比数列,修正项的下一项应为-16,则( )
=8*24-16=192-16=176,对应B项。【选B】
5.做商数列
1.概述
1.题型特征:任意相邻两项之间倍数关系明显。
2.解题方法:两两做商找规律。
3.注意点:
(1)做商时注意方向。
(2)商有正有负、有整数有分数有小数(6 和 15 同时出现,15/6=2.5)
2.例子
例1(2016深圳)1,1,3,15,105,( )
A.765 B.742 C.903 D.945
【解析】例1.倍数关系明显,考虑两两做商找规律,做商后得:1、3、5、7,
下一项应为9,( )=105*9=945,对应D项。【选D】
例3(2014广州)2,-8,24,-48,48,( )
A.-96 B.-32 C.0 D.64
【解析】例3.倍数关系明显,做商:-4、-3、-2、-1,下一项应为0,( )
/48=0,则( )=0,对应C项。【选C】
例4(2014河北)2,6,15,30,45,( )
A.63 B.57 C.51 D.45
【解析】例4.倍数关系明显,做商:3、2.5、2、1.5,下一项应为1,( )
/45=1,( )=45,对应D项。【选D】
6.幂次数列
1.概述
1.题型特征:本身或附近有幂次数(64 比较热门)。
2.解题方法:
(1)普通幂次——直接找规律。
(2)修正幂次——先转化为普通幂次±修正项,再找规律。
3.注意点:
(1)从唯一变化入手(避开变化多端的数字:1,16,64,81)。
(2)负幂次(1/7=7-1,1/7²=7-2)。
(3)修正项(-5~5)小,从 64 入手
2.例子
例 1(2017 上海)1,32,81,64,25,( )
A.12 B.10 C.8 D.6
【解析】例 1.幂次数列,先还原,优先还原 25=5²,32=25,推导:2 和中间
空了两处,大胆猜测为 2、3、4、5,81=9²=34,64=4³,可知规律为:底数:2、
3、4、5、6,指数为 5、4、3、2、1,( )=61=6,对应 D 项。【选 D】
【注意】1=16
例 3(2017 深圳)1,–3,4,1,25,( )
A.15 B.100 C.325 D.676
【解析】例 3.4、1、25 是幂次数,从幂次切入:25=5²,4=2²,2 和 5 中间
只有一个空,填 3 或 4 均不合适,需要推断:4+1=5,( 4+1)²=5²=25,即(①+
②)²=③,验证规律:(1-3)²=(-2)²=2²=4,(-3+4)²=1²=1,规律成立,则
(1+25)²=26²,尾数为 6,对应 D 项。【选 D】
例 4(2018 浙江)5,7,4,9,25,( )
A.49 B.121 C.189 D.256
【解析】例 4.4、9、25 均是幂次数,考虑幂次:4=2²,9=3²,25=5²。 (5-7)
²=2²=4, (7-4)²=3²=9,( 4-9)²=5²=25,则( )=(9-25)²=(-16)²=16²=256,
或求得尾数为 6,对应 D 项。【选 D】
例 5(2018 广州)3,11,13,29,( )
A.31 B.34
C.38 D.41
【解析】例 5.本题做差无规律,考虑递推,但只有 4 项不好递推,考虑幂
次数列。找出数列周围的幂次数:29 周围的幂次数为 25=5²,13 周围的幂次数
为 16=4²,11 周围的幂次数为 9=3²,3 周围的幂次数为 4=2²,找出修正项:
25+4=29,16-3=13,9+2=11,4-1=3,则修正项为:-1、+2、-3、+4、-5,( )
=6²-5=31,对应 A 项。【选 A】
【注意】出题人爱考的幂次数为 64:64 变化多端,64=8²=4³=26,且数列趋
势均为从大到小或从小到大,都有可能经过 64,因此 64 相当于幂次数列的网红数字
7.分数数列
1.概述
1.题型特征:全部或大部分是分数。
2.解题方法:先观察分子、分母是否递增或递减。
(1)是:先分开看,再一起看。
(2)否:反约分变为递增(规律一致)。
3.注意点:
(1)通过分子或分母直接锁定答案。
(2)反约分从数列中间的入手。
(3)分子或分母容易统一想大通分。
反约分变为递增。如 1/3,2/4,3/5,4/6,可知下一项为 5/7,
但出题人不会出这么简单,利用分数性质:2/4=1/2,4/6=2/3,此时数列变为:
1/3、1/2、3/5、2/3,找规律较难,即出题人会通过约分增加难度,做题时考虑
先反约分(变为递增或递减),再找规律。
2.举例
例 1(2015 深圳)1/2,4/7,7/12,10/17,( )
A.11/20 B.12/21 C.13/22 D.14/23
【解析】例 1.方法一:分数数列,分子:1、4、7、10,为公差为 3 的等差
数列,分母:2、7、12、17,为公差为 5 的等差数列,( )=(10+3)/(17+5)
=13/22,对应 C 项。
例 2(2018 江苏)1,2,3/2,5/6,11/30,( )
A.17/90 B.23/180 C.37/240 D.41/330
【解析】例 2.分数数列,单独看无规律,联合看:2+3=5,6+5=11,( )
处分子=30+11=41,41 无法约分为 17、23、37,排除 A、B、C 项,对应 D 项。【选
D】
例 3(2017 江苏)1/3,1/2,3/7,5/11,4/9,( )
A.13/29 B.11/27 C.9/25 D.15/31
【解析】例 3.分子、分母不是递增或递减的规律,1/2 和 4/9 影响了递增规
律,考虑反约分:优先反约分 1/2(反约分可能性很多,只要分子、分母符合两
倍关系即可,但观察后发现 1/2 夹在两数中间,此时容易确认反约分后的数值,
即反约分优先反约分夹在中间的),1/2=2/4。找规律:分子变为 1、2、3、5,
分母变为 3、4、7、11,分子为递推和数列,分母为递推和数列,则下一项
=8/18=4/9,说明规律正确,则( )=13/29,对应 A 项。【选 A】
例 5(2018 浙江)1/16,1/7,1/4,2/5,5/8,( )
A.6/7 B.1 C.3/2 D.2
【解析】例 5.分子呈递增趋势,分母从 16→8 为递减趋势,反约分时要兼
顾两个规律,分子要想递增,则 1/7 变为 2/14,1/4 变为 3/12,2/5 变为 4/10,
分子变为 1、2、3、4、5(递增),分母变为 16、14、12、10、8(递减),则( )
=6/6=1,对应 B 项。【选 B】
例 6(2017 广州)2,1,2/3,1/2,2/5,1/3,( )
A.2/7 B.1/4 C.5/2 D.1
【解析】例 6.分子、分母为交叉变化规律,既不是递增又不是递减,此时
考虑统一规律或大通分(将分子或分母统一起来),将分子变为相同:2/1、2/2、
2/3、2/4、2/5、2/6,则( )=2/7,对应 A 项。【选 A】
【注意】既没有递增也没有递减规律时,考虑大通分(兜底方法)。
8.多重数列
1.概述
1.题型特征:项数多(≥6 项)。
2.解题方法:先交叉(奇数项和偶数项分开看)再分组(两两分组)。如 2、
4、3、6、4、8,两两分组,均为 2 倍关系
2.举例
例 1(2018 新疆)2,2,5,4,8,6,11,8,14,10,( )
A.15 B.17 C.12 D.16
【解析】例 1.数列较长,先交叉后分组。奇数项:2、5、8、11、14、( ),
为公差为 3 的等差数列,则( )=14+3=17,对应 B 项。【选 B】
【注意】1.偶数项:2、4、6、8、10,为公差为 2 的等差数列。
例 2(2015 浙江)2,3,4,9,16,45,( ),315
A.90 B.96 C.102 D.120
【解析】例 2.数列长,考虑多重数列,奇数项:2、4、16、( ),倍数关
系明显,做商得:2、4、则( )/16 大概率结果为 6,偶数项:3、9、45、315,
做商得:3、5、7,为等差数列,因此规律比较严谨,( )=16*6=96,对应 B
项。【选 B】
例 5(2018 江苏)2.1,5.2,8.4,11.8,14.16,( )
A.19.52 B.19.24 C.17.82 D.17.32
【解析】例 5.数列小数点多,做差无规律,考虑拆分,“.”起连接作用, “.”
前:2、5、8、11、14,为公差为 3 的等差数列,则下一项为 17;“ .”后:1、2、
4、8、16,下一项为 32,因此( )=17.32,对应 D 项。【选 D】
【注意】出题人有时候也会省略“.”。
例 6(2018 深圳)1716,2523,3330,4642,5853,( )
A.6862 B.6765 C.6662 D.6460
【解析】例 6.四位数出现时千万不要做差,考虑拆分,从中间拆开,17、
25、33、46、58,做差:8、8、13、12,单独看没有规律,考虑联合看,即内部
分组找规律:17 和 16 差 1,25 和 23 差 2,33 和 30 差 3,46 和 42 差 4,58 和
53 差 5,下一项差 6,A 项:68-62=6,保留;B 项:67-65≠6,排除;C 项:66-62
≠6,排除;D 项:64-6≠6,排除,A 项当选。【选 A】
【注意】用好“拆”字诀,快速求解





